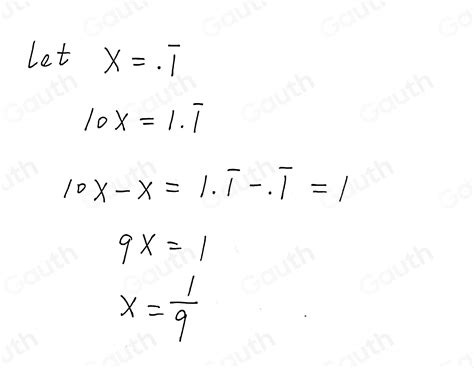Converting 0.24 Repeating to a Fraction in Simplest Form

Converting a repeating decimal to a fraction can be a bit tricky, but it's a useful skill to have, especially in mathematics and science. In this article, we'll explore how to convert the repeating decimal 0.24 to a fraction in simplest form.
Understanding Repeating Decimals
A repeating decimal is a decimal number that goes on forever in a repeating pattern. For example, 0.24 repeating means that the decimal 0.242424... goes on forever. To convert a repeating decimal to a fraction, we need to identify the repeating pattern and use it to create an equation.
Converting 0.24 Repeating to a Fraction

To convert 0.24 repeating to a fraction, let's follow these steps:
- Let x = 0.242424...
- Multiply both sides of the equation by 100 to eliminate the repeating decimal: 100x = 24.242424...
- Subtract the original equation from the new equation: 100x - x = 24.242424... - 0.242424...
- Simplify the equation: 99x = 24
- Divide both sides of the equation by 99: x = 24/99
Simplifying the Fraction
The fraction 24/99 can be simplified further by dividing both the numerator and denominator by 3. This gives us:
- 24 ÷ 3 = 8
- 99 ÷ 3 = 33
So, the simplified fraction is 8/33.
Verifying the Answer

To verify that 8/33 is indeed the correct fraction, we can convert it back to a decimal:
- 8 ÷ 33 = 0.242424...
This matches the original repeating decimal, so we can be confident that our answer is correct.
Conclusion and Future Applications
Converting repeating decimals to fractions is an important skill in mathematics, and it's used in a variety of real-world applications, such as finance, science, and engineering. By mastering this skill, you'll be able to tackle more complex problems and calculations with ease.
In the future, you may encounter more complex repeating decimals, such as 0.123123... or 0.456456.... By following the same steps outlined in this article, you'll be able to convert these decimals to fractions in simplest form.
Practical Examples and Applications

Converting repeating decimals to fractions has many practical applications, such as:
- Calculating interest rates and investments
- Determining the cost of goods and services
- Measuring quantities in science and engineering
- Solving complex mathematical problems
By understanding how to convert repeating decimals to fractions, you'll be able to tackle these applications with confidence and accuracy.
Summary and Key Takeaways
In this article, we've explored how to convert the repeating decimal 0.24 to a fraction in simplest form. By following the steps outlined above, you can convert any repeating decimal to a fraction. Remember to:
- Identify the repeating pattern
- Create an equation
- Simplify the fraction
- Verify the answer
By mastering this skill, you'll be able to tackle more complex mathematical problems and applications with ease.
What is a repeating decimal?
+A repeating decimal is a decimal number that goes on forever in a repeating pattern.
How do I convert a repeating decimal to a fraction?
+To convert a repeating decimal to a fraction, identify the repeating pattern, create an equation, simplify the fraction, and verify the answer.
What are some practical applications of converting repeating decimals to fractions?
+Converting repeating decimals to fractions has many practical applications, such as calculating interest rates and investments, determining the cost of goods and services, measuring quantities in science and engineering, and solving complex mathematical problems.
We hope this article has been helpful in explaining how to convert 0.24 repeating to a fraction in simplest form. If you have any further questions or would like to explore more mathematical concepts, please don't hesitate to ask!