Slope Intercept Form: X3y3 Made Easy

Quick Links :

Understanding the slope-intercept form of a linear equation is crucial for anyone learning algebra or preparing for standardized tests like the SAT or ACT. In this article, we'll break down the concept of slope-intercept form, provide examples, and offer tips for working with this essential math concept.

What is Slope-Intercept Form?

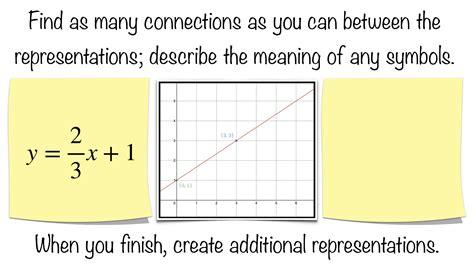
The slope-intercept form is a way of writing a linear equation in the form y = mx + b, where:

• m is the slope of the line
• b is the y-intercept (the point where the line crosses the y-axis)
• x is the independent variable (the value that changes)
• y is the dependent variable (the value that depends on x)

This form is useful because it allows us to easily identify the slope and y-intercept of a line, which can be helpful in graphing and solving equations.

How to Write an Equation in Slope-Intercept Form

Writing an equation in slope-intercept form is relatively straightforward. If you know the slope (m) and the y-intercept (b), you can simply plug them into the equation y = mx + b.

For example, if the slope is 2 and the y-intercept is 3, the equation would be:

y = 2x + 3

On the other hand, if you're given an equation in a different form, such as standard form (Ax + By = C), you'll need to rearrange it to isolate y. Here's an example:

2x + 3y = 6

To convert this equation to slope-intercept form, we need to isolate y:

3y = -2x + 6

y = (-2/3)x + 2

As you can see, the slope is -2/3 and the y-intercept is 2.

Key Benefits of Slope-Intercept Form

There are several benefits to using the slope-intercept form:

• Easy to graph: With the slope and y-intercept, you can quickly graph a line.
• Simplifies solving equations: Slope-intercept form makes it easier to solve equations by isolating y.
• Helps with word problems: Slope-intercept form is useful for solving word problems that involve linear relationships.
• Builds foundation for advanced math: Understanding slope-intercept form is crucial for more advanced math concepts, such as linear algebra and calculus.

Common Applications of Slope-Intercept Form

Slope-intercept form has numerous applications in various fields, including:

• Physics and engineering: To model the motion of objects and forces.
• Economics: To represent supply and demand curves.
• Computer science: To optimize algorithms and model complex systems.
• Data analysis: To create linear models and make predictions.

Working with Slope-Intercept Form: Tips and Tricks

Here are some tips and tricks for working with slope-intercept form:

• Use the slope-intercept form to check your answers: When solving equations, plug your solution back into the original equation to ensure it's true.
• Pay attention to the signs: Make sure to keep track of the signs of the slope and y-intercept, as they can affect the graph and solution.
• Practice, practice, practice: The more you work with slope-intercept form, the more comfortable you'll become.
• Use graphing calculators or software: Graphing calculators or software can help you visualize the line and check your work.

Real-World Examples of Slope-Intercept Form

Here are some real-world examples of slope-intercept form:

• Cost-benefit analysis: A company is considering a new project that will cost $100,000 to implement and is expected to generate $50,000 in revenue per year. If the project is expected to last for 5 years, the equation representing the total revenue (y) in terms of the number of years (x) is y = 50,000x - 100,000.
• Population growth: A city's population is growing at a rate of 2% per year. If the current population is 100,000, the equation representing the population (y) in terms of the number of years (x) is y = 100,000(1.02)^x.

Common Mistakes to Avoid

When working with slope-intercept form, be aware of the following common mistakes:

• Forgetting to distribute the slope: Make sure to distribute the slope to both terms in the equation.
• Incorrectly identifying the y-intercept: Double-check that you've correctly identified the y-intercept.
• Mixing up the signs: Pay attention to the signs of the slope and y-intercept, as they can affect the graph and solution.

Conclusion and Next Steps

In conclusion, slope-intercept form is a powerful tool for working with linear equations. By understanding the concept and applying the tips and tricks outlined in this article, you'll be well on your way to mastering slope-intercept form.

If you're looking to further develop your math skills, we recommend exploring other topics, such as quadratic equations, functions, and graphing. With practice and dedication, you'll become proficient in using slope-intercept form and be able to tackle more complex math concepts.