5 Ways To Write Slope Intercept Form From A Graph

Quick Links :

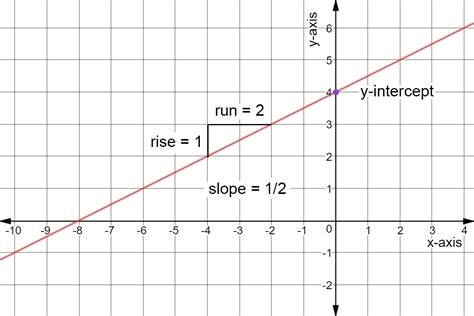
Graphs are a powerful tool for visualizing relationships between variables, and being able to write the equation of a line in slope-intercept form from a graph is a fundamental skill in mathematics and science. Slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept, is one of the most common and useful forms of a linear equation. Here, we'll explore five ways to write slope-intercept form from a graph, along with practical examples and tips.

Method 1: Finding the Slope and Y-Intercept Directly from the Graph

One of the simplest ways to write slope-intercept form from a graph is to directly identify the slope (m) and the y-intercept (b) from the graph. To find the slope, look for two points on the line and calculate the rise over run. The y-intercept is the point where the line crosses the y-axis.

For example, consider the graph of a line that passes through the points (2, 3) and (4, 5). The rise between these points is 2 (5 - 3), and the run is 2 (4 - 2), so the slope (m) is 2/2 = 1. The y-intercept (b) can be seen as 1, where the line crosses the y-axis. Therefore, the equation of the line in slope-intercept form is y = x + 1.

Tips for Method 1:

• Make sure to choose two points that are clearly on the line to avoid errors in calculating the slope.
• If the line crosses the y-axis at a point that is not clearly visible, you might need to use another method to find the y-intercept.

Method 2: Using the Slope Formula and Finding the Y-Intercept

If the graph does not clearly show the y-intercept, or if you prefer a more algebraic approach, you can use the slope formula to find the slope of the line and then find the y-intercept. The slope formula is m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are any two points on the line.

Once you have the slope, substitute one of the points into the equation y = mx + b to solve for b, the y-intercept.

For example, using the same graph as above, the slope (m) is 1. If we use the point (2, 3) and substitute it into the equation, we get 3 = 1(2) + b, which simplifies to b = 1. Therefore, the equation of the line in slope-intercept form is y = x + 1.

Tips for Method 2:

• Ensure that the points you choose are accurately read from the graph to avoid calculation errors.
• This method is particularly useful when the y-intercept is not clearly visible on the graph.

Method 3: Using the Point-Slope Form as an Intermediate Step

Another approach is to first write the equation of the line in point-slope form, y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope. Once in point-slope form, you can easily rearrange the equation into slope-intercept form.

For example, if we know the line passes through (2, 3) and has a slope of 1, the point-slope form is y - 3 = 1(x - 2). Rearranging, we get y = x + 1, which is the equation of the line in slope-intercept form.

Tips for Method 3:

• This method is useful if you're more comfortable with the point-slope form or if the graph clearly shows a point and the slope.
• Be careful when rearranging the equation to avoid algebraic mistakes.

Method 4: Graphical Analysis for Parallel and Perpendicular Lines

When dealing with parallel or perpendicular lines, graphical analysis can provide insights into their equations. Parallel lines have the same slope but different y-intercepts. Perpendicular lines have slopes that are negative reciprocals of each other.

If you're given a graph with parallel or perpendicular lines, you can use the relationship between their slopes and the given information to write their equations in slope-intercept form.

For example, if a line is parallel to y = x + 1 and passes through (3, 4), knowing that parallel lines have the same slope allows you to write the equation as y = x + b. Substituting (3, 4) into the equation gives you b = 1. Therefore, the equation of the parallel line is y = x + 1.

Tips for Method 4:

• Pay close attention to the relationship between the slopes of parallel and perpendicular lines.
• This method is particularly useful in problems involving multiple lines and their relationships.

Method 5: Using Technology to Find the Equation of a Line

In today's digital age, graphing calculators and computer software can be powerful tools for finding the equation of a line from a graph. These tools can calculate the slope and y-intercept directly from the graph, providing the equation in slope-intercept form.

For instance, using a graphing calculator, you can enter the graph of the line and use the calculator's built-in functions to find the slope and y-intercept. This method is especially useful for more complex graphs or when accuracy is paramount.

Tips for Method 5:

• Familiarize yourself with the specific functions of your graphing calculator or software.
• Double-check the calculator's output to ensure accuracy.

Now that you've explored these five methods for writing slope-intercept form from a graph, take a moment to reflect on which method(s) you find most intuitive or useful. Whether you prefer a direct graphical approach, an algebraic method, or leveraging technology, mastering these techniques will enhance your ability to analyze and work with linear equations.

Don't forget to practice these methods with various graphs to solidify your understanding. And if you have any questions or insights, feel free to share in the comments below!