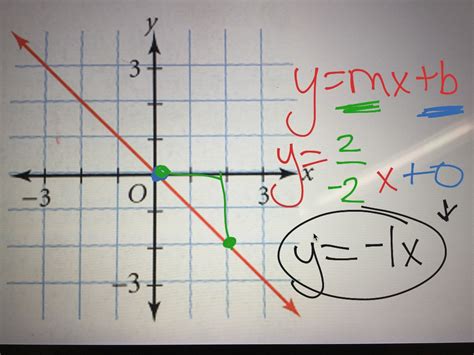5 Ways To Write Equations From Graphs Easily

Quick Links :

Writing equations from graphs can seem like a daunting task, but with the right strategies, it can be done easily and efficiently. In this article, we will explore five ways to write equations from graphs, helping you to become more confident in your math skills.

When working with graphs, it's essential to understand the different types of equations that can be represented. From linear to quadratic, and even polynomial equations, each type has its unique characteristics. By recognizing these characteristics, you can identify the equation that corresponds to a given graph.

Understanding the Basics of Graphs

Before diving into the five ways to write equations from graphs, let's review some basic concepts. A graph is a visual representation of a relationship between two variables, typically x and y. The x-axis represents the input or independent variable, while the y-axis represents the output or dependent variable. The graph shows the behavior of the function, including its zeros, intercepts, and turning points.

Key Components of a Graph

When analyzing a graph, look for the following key components:

• X-intercepts: The points where the graph crosses the x-axis.
• Y-intercepts: The points where the graph crosses the y-axis.
• Zeros: The values of x that make the function equal to zero.
• Turning points: The points where the graph changes direction.
• Asymptotes: The lines that the graph approaches but never touches.

Method 1: Identifying Linear Equations

Linear equations are the simplest type of equation and can be easily identified from a graph. A linear equation has the form y = mx + b, where m is the slope and b is the y-intercept. To write a linear equation from a graph, follow these steps:

1. Identify the y-intercept: Look for the point where the graph crosses the y-axis.
2. Identify the slope: Calculate the slope by finding the ratio of the change in y to the change in x.
3. Write the equation: Use the slope-intercept form to write the equation, y = mx + b.

Example: The graph shows a linear equation with a y-intercept of 2 and a slope of 3. The equation is y = 3x + 2.

Method 2: Identifying Quadratic Equations

Quadratic equations have the form y = ax^2 + bx + c, where a, b, and c are constants. To write a quadratic equation from a graph, follow these steps:

1. Identify the vertex: Look for the turning point of the graph.
2. Identify the x-intercepts: Look for the points where the graph crosses the x-axis.
3. Write the equation: Use the vertex form to write the equation, y = a(x - h)^2 + k.

Example: The graph shows a quadratic equation with a vertex of (2, 3) and x-intercepts of 1 and 3. The equation is y = (x - 2)^2 + 3.

Method 3: Using the Point-Slope Form

The point-slope form is a useful method for writing equations from graphs. This method uses the slope and a point on the graph to write the equation. To use the point-slope form, follow these steps:

1. Identify a point on the graph: Choose any point on the graph.
2. Calculate the slope: Calculate the slope using the point and another point on the graph.
3. Write the equation: Use the point-slope form to write the equation, y - y1 = m(x - x1).

Example: The graph shows a linear equation with a point of (2, 3) and a slope of 2. The equation is y - 3 = 2(x - 2).

Method 4: Using the Slope-Intercept Form

The slope-intercept form is another useful method for writing equations from graphs. This method uses the slope and the y-intercept to write the equation. To use the slope-intercept form, follow these steps:

1. Identify the y-intercept: Look for the point where the graph crosses the y-axis.
2. Calculate the slope: Calculate the slope using two points on the graph.
3. Write the equation: Use the slope-intercept form to write the equation, y = mx + b.

Example: The graph shows a linear equation with a y-intercept of 1 and a slope of 4. The equation is y = 4x + 1.

Method 5: Using Graphing Software

Graphing software is a powerful tool for writing equations from graphs. Many graphing software programs can identify the equation of a graph and display it on the screen. To use graphing software, follow these steps:

1. Enter the graph: Enter the graph into the software program.
2. Identify the equation: Use the software program to identify the equation of the graph.
3. Write the equation: Write the equation using the software program's output.

Example: The graph shows a quadratic equation with a vertex of (2, 3) and x-intercepts of 1 and 3. The software program identifies the equation as y = (x - 2)^2 + 3.

In conclusion, writing equations from graphs can be done easily and efficiently using the five methods outlined in this article. By understanding the basics of graphs, identifying key components, and using the right strategies, you can become more confident in your math skills.