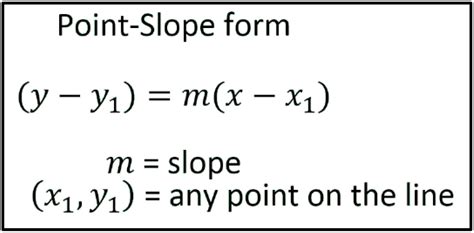Write Equation Of Line In Point Slope Form Easily

Quick Links :

Finding the equation of a line in point-slope form is a fundamental concept in mathematics, particularly in algebra and geometry. It's a simple yet powerful tool for defining lines on a coordinate plane. The point-slope form is one of the several ways to represent a line, alongside slope-intercept form and standard form. This article will guide you through understanding what the point-slope form is, its components, and how to easily write the equation of a line using this form.

Understanding Point-Slope Form

The point-slope form of a line is given by the formula: y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope of the line. The slope indicates how steep the line is, with positive slopes indicating lines that rise from left to right, negative slopes indicating lines that fall from left to right, and zero slope indicating a horizontal line.

Components of Point-Slope Form

• Point (x1, y1): This is any point that lies on the line. The coordinates (x1, y1) are used in the equation.
• Slope (m): The slope is a measure of the line's steepness. It can be calculated using the formula m = (y2 - y1) / (x2 - x1) if two points (x1, y1) and (x2, y2) on the line are known.

How to Write the Equation of a Line in Point-Slope Form

Writing the equation of a line in point-slope form involves knowing a point on the line and the slope of the line. Here's a step-by-step guide:

1. Identify a Point on the Line: You need to know at least one point that the line passes through. This point can be given, found from a graph, or derived from another equation of the line.

2. Determine the Slope of the Line: If you have two points, you can calculate the slope using the slope formula. Alternatively, the slope can be given, or it might be derived from the graph or another equation.

3. Apply the Point-Slope Formula: Once you have a point (x1, y1) and the slope (m), you can directly plug these values into the point-slope formula: y - y1 = m(x - x1).

Example of Writing an Equation in Point-Slope Form

Suppose we want to write the equation of a line that passes through the point (3, 4) and has a slope of 2.

1. Identify the Point and Slope: Point (x1, y1) = (3, 4) and slope (m) = 2.
2. Apply the Point-Slope Formula: Substitute the point and slope into the formula to get y - 4 = 2(x - 3).

This equation represents the line in point-slope form. It shows that for any point on the line, the difference between the y-coordinate and 4 is equal to twice the difference between the x-coordinate and 3.

Benefits of Point-Slope Form

The point-slope form has several benefits:

• Ease of Use: It's straightforward to write an equation in point-slope form if you know a point on the line and the slope.
• Applicability: This form is particularly useful for finding equations of lines when you have a point and the slope or when you're working with graphs and need to identify specific lines.

Challenges and Solutions

Some challenges you might face when working with point-slope form include:

• Difficulty in Finding the Slope: If you don't have the slope, finding it can be challenging, especially without two points or additional information about the line.
• Accuracy in Substitution: Care must be taken when substituting values into the point-slope formula to avoid errors.

To overcome these challenges, ensure you carefully follow the steps for calculating the slope if needed, and double-check your substitution into the formula.

Conclusion and Final Thoughts

Writing the equation of a line in point-slope form is a fundamental skill in mathematics that can be easily mastered with practice. By understanding the components of the point-slope form and following the simple steps outlined in this article, you can confidently write equations of lines in this form. Remember, the key to success lies in accurately identifying a point on the line and determining the slope, which can then be straightforwardly applied to the point-slope formula.

We hope this comprehensive guide has helped you grasp the concept of writing equations of lines in point-slope form. If you have any questions or need further clarification, please don't hesitate to ask in the comments section below. Share this article with friends or classmates who might find it helpful, and don't forget to explore other mathematical concepts to deepen your understanding of algebra and geometry.