5 Ways To Write Exponential Form

Quick Links :

Expressing numbers in exponential form is a fundamental concept in mathematics, particularly in algebra and calculus. It provides a concise way to represent large or small numbers using a base and an exponent. Mastering the art of writing numbers in exponential form can simplify complex calculations and enhance problem-solving skills.

Understanding Exponential Form

In exponential form, a number is expressed as a product of a base and an exponent. The base can be any positive number, while the exponent indicates the power to which the base should be raised. For instance, the number 2^3 represents 2 raised to the power of 3, which equals 8.

Why Exponential Form Matters

Writing numbers in exponential form has numerous benefits. It helps to:

• Simplify complex calculations by reducing the need for repeated multiplication
• Represent large or small numbers in a more compact and readable format
• Facilitate algebraic manipulations and calculations
• Enhance understanding of mathematical concepts, such as exponential growth and decay

Method 1: Identifying the Base and Exponent

When expressing a number in exponential form, it's essential to identify the base and exponent correctly. The base is the number being multiplied, while the exponent is the number of times the base is multiplied by itself.

For example, the number 4^2 can be broken down into its base (4) and exponent (2). This means that 4 is multiplied by itself 2 times, resulting in 16.

Example: Writing 16 in Exponential Form

To write 16 in exponential form, we can identify the base as 4 and the exponent as 2.

16 = 4^2

Method 2: Using the Definition of Exponents

Another way to write a number in exponential form is by using the definition of exponents. This involves expressing the number as a product of the base and the exponent.

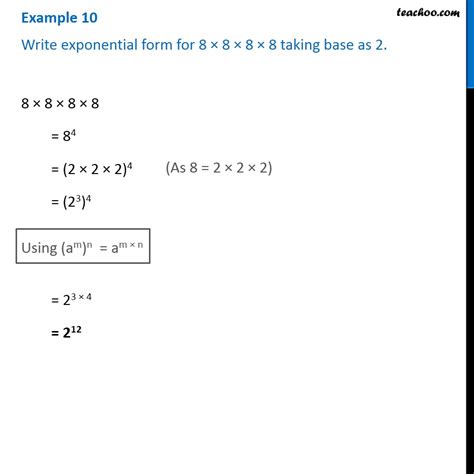
For instance, the number 8 can be written as 2^3 using the definition of exponents.

8 = 2 × 2 × 2 = 2^3

Example: Writing 27 in Exponential Form

To write 27 in exponential form, we can use the definition of exponents.

27 = 3 × 3 × 3 = 3^3

Method 3: Simplifying Expressions with Exponents

When simplifying expressions with exponents, it's essential to apply the rules of exponents correctly. This includes multiplying exponents with the same base and adding exponents with the same base.

For example, the expression 2^2 × 2^3 can be simplified by adding the exponents.

2^2 × 2^3 = 2^(2+3) = 2^5

Example: Simplifying 4^2 × 4^3

To simplify the expression 4^2 × 4^3, we can add the exponents.

4^2 × 4^3 = 4^(2+3) = 4^5

Method 4: Converting from Standard Form to Exponential Form

Converting numbers from standard form to exponential form involves identifying the base and exponent. This can be done by analyzing the number's prime factorization.

For instance, the number 48 can be converted to exponential form by identifying its prime factors.

48 = 2^4 × 3

Example: Converting 72 to Exponential Form

To convert 72 to exponential form, we can identify its prime factors.

72 = 2^3 × 3^2

Method 5: Using Exponential Form to Simplify Calculations

Finally, exponential form can be used to simplify complex calculations involving large or small numbers. By expressing numbers in exponential form, we can reduce the need for repeated multiplication and make calculations more manageable.

For example, the calculation 2^3 × 2^4 can be simplified using exponential form.

2^3 × 2^4 = 2^(3+4) = 2^7

Example: Simplifying 3^2 × 3^5

To simplify the calculation 3^2 × 3^5, we can use exponential form.

3^2 × 3^5 = 3^(2+5) = 3^7

We hope this article has helped you understand the different methods for writing numbers in exponential form. By mastering these techniques, you'll become proficient in simplifying complex calculations and solving problems involving exponents.

We encourage you to share your thoughts and questions in the comments below. How do you apply exponential form in your everyday life? What are some common mistakes to avoid when working with exponents?