Convert To Vertex Form In 3 Easy Steps

Quick Links :

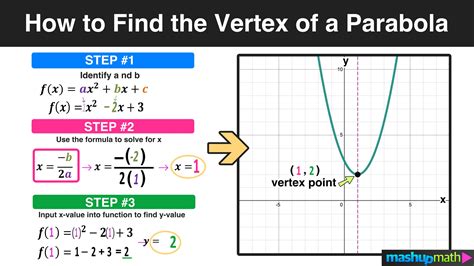
Converting equations to vertex form is a fundamental concept in algebra and geometry. The vertex form of a quadratic equation is particularly useful for graphing parabolas, as it immediately reveals the vertex of the parabola. In this article, we will explore the process of converting quadratic equations to vertex form in three easy steps.

Why Convert to Vertex Form?

Converting a quadratic equation to vertex form can be incredibly useful in a variety of situations. For one, it allows you to easily identify the vertex of the parabola, which can be a crucial piece of information in graphing and solving problems. Additionally, vertex form can make it simpler to determine the axis of symmetry, x-intercepts, and other key features of the parabola.

Real-World Applications

The vertex form of a quadratic equation has numerous real-world applications. For instance, it can be used to model the trajectory of projectiles, the shape of satellite dishes, and even the design of roller coasters. By converting equations to vertex form, you can gain a deeper understanding of these complex systems and make more accurate predictions.

Step 1: Write the Equation in Standard Form

The first step in converting a quadratic equation to vertex form is to write the equation in standard form. The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants.

For example, consider the equation x^2 + 5x + 6 = 0. This equation is already in standard form, so we can move on to the next step.

Completing the Square

If the equation is not in standard form, you may need to complete the square to rewrite it in the correct form. Completing the square involves moving the constant term to the right-hand side of the equation and then adding and subtracting the square of half the coefficient of x to the left-hand side.

Step 2: Complete the Square

The second step in converting a quadratic equation to vertex form is to complete the square. To do this, we will add and subtract the square of half the coefficient of x to the left-hand side of the equation.

Using the example equation x^2 + 5x + 6 = 0, we can complete the square as follows:

x^2 + 5x + 6 = 0 x^2 + 5x = -6 x^2 + 5x + (5/2)^2 = -6 + (5/2)^2 (x + 5/2)^2 = -6 + 25/4

The Vertex Form Takes Shape

At this point, we can start to see the vertex form of the equation taking shape. The equation is now in the form (x - h)^2 = k, where (h, k) is the vertex of the parabola.

Step 3: Write the Equation in Vertex Form

The final step in converting a quadratic equation to vertex form is to write the equation in the correct format. The vertex form of a quadratic equation is (x - h)^2 = k, where (h, k) is the vertex of the parabola.

Using the example equation, we can write the vertex form as follows:

(x + 5/2)^2 = -6 + 25/4 (x + 5/2)^2 = 1/4 (x + 5/2)^2 - 1/4 = 0

Identifying the Vertex

Now that we have the equation in vertex form, we can easily identify the vertex of the parabola. The vertex is located at the point (h, k), where h is the value that is being subtracted from x and k is the constant term.

In this case, the vertex is located at the point (-5/2, -1/4).

By following these three easy steps, you can convert any quadratic equation to vertex form and gain a deeper understanding of the underlying mathematics. Whether you're a student, teacher, or simply a math enthusiast, mastering the art of converting to vertex form is an essential skill that will serve you well in a variety of situations.