Parabola Vertex Form Equation Calculator Guide

Quick Links :

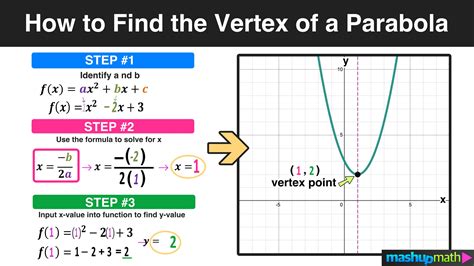
Understanding the concept of parabolas and their equations is crucial in mathematics, particularly in algebra and calculus. One of the most convenient forms of a parabola equation is the vertex form, which provides immediate information about the parabola's vertex, axis of symmetry, and direction of opening. In this article, we will delve into the world of parabolas, exploring what they are, their importance, and how to work with them, especially focusing on the vertex form equation and its applications.

What is a Parabola?

A parabola is a U-shaped curve that is a result of a quadratic equation. It is a type of conic section that is formed by the intersection of a cone and a plane. Parabolas are symmetric about their axis, which passes through the vertex. The vertex is the lowest or highest point of the parabola, and the axis of symmetry divides the parabola into two equal parts.

Importance of Parabolas in Real Life

Parabolas are not just theoretical concepts; they have numerous practical applications in various fields. For instance, parabolas are used in the design of satellite dishes, mirrors, and headlights because of their ability to focus light and signals. In physics, parabolas describe the path of projectiles under the influence of gravity. Moreover, parabolas are essential in mathematics for solving quadratic equations, which model a wide range of real-world phenomena.

Standard Form of a Parabola Equation

The standard form of a parabola equation is y = ax^2 + bx + c, where a, b, and c are constants. However, this form does not provide immediate insight into the parabola's key features, such as its vertex and axis of symmetry.

Why Vertex Form?

The vertex form of a parabola equation, y = a(x - h)^2 + k, is particularly useful because it directly gives the coordinates of the vertex (h, k) and the direction of the parabola's opening. The coefficient 'a' determines the parabola's shape and direction, with a > 0 indicating a parabola that opens upwards and a < 0 indicating a parabola that opens downwards.

How to Convert Standard Form to Vertex Form

Converting a parabola equation from standard form to vertex form involves completing the square, a process that rearranges the equation to isolate the squared term.

1. Start with the standard form equation: y = ax^2 + bx + c.
2. Move the constant term to the right side: y - c = ax^2 + bx.
3. Factor out the coefficient of x^2: y - c = a(x^2 + bx/a).
4. Add and subtract (b/2a)^2 inside the parenthesis: y - c = a(x^2 + bx/a + (b/2a)^2 - (b/2a)^2).
5. Write the expression inside the parenthesis as a perfect square: y - c = a(x + b/2a)^2 - a(b/2a)^2.
6. Simplify and rearrange to vertex form: y = a(x - (-b/2a))^2 + c - a(b/2a)^2.

Example: Converting to Vertex Form

Consider the equation y = 2x^2 + 4x + 3. Following the steps:

1. y - 3 = 2x^2 + 4x
2. y - 3 = 2(x^2 + 2x)
3. y - 3 = 2(x^2 + 2x + 1 - 1)
4. y - 3 = 2(x^2 + 2x + 1) - 2
5. y - 3 = 2(x + 1)^2 - 2
6. y = 2(x + 1)^2 + 1

The vertex form equation is y = 2(x + 1)^2 + 1, with the vertex at (-1, 1).

Using a Parabola Vertex Form Equation Calculator

While converting to vertex form can be done manually, using a parabola vertex form equation calculator can significantly reduce the time and effort involved. These calculators typically ask for the coefficients of the standard form equation and then output the vertex form equation and other relevant details such as the vertex, axis of symmetry, and the direction of the parabola.

Benefits of Using a Calculator

• Efficiency: Quick conversion to vertex form without the need to manually complete the square.
• Accuracy: Reduces the likelihood of human error, ensuring the vertex form equation is accurate.
• Saves Time: Allows for faster analysis and graphing of parabolas.

Conclusion

Parabolas are fundamental in mathematics, and understanding their equations, especially in vertex form, is crucial for various applications. The vertex form provides immediate insight into the parabola's key features, making it easier to analyze and graph. While manual conversion to vertex form is possible, using a parabola vertex form equation calculator is a more efficient, accurate, and time-saving approach. By leveraging such tools, one can focus on deeper mathematical analysis and real-world applications.

Now, we invite you to share your thoughts on the importance of parabolas in mathematics and their applications in real life. Have you used a parabola vertex form equation calculator? How did it help in your studies or projects? Your feedback and insights are valuable, so please feel free to comment below.