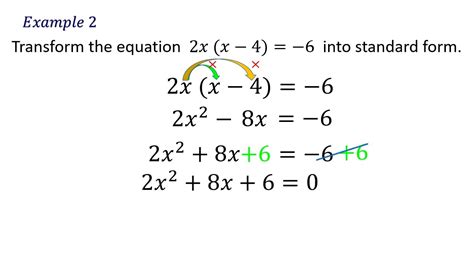Write A Quadratic Equation In Standard Form Easily

Quick Links :

Understanding quadratic equations is a crucial part of algebra, and writing them in standard form is a fundamental skill that can simplify solving problems. A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable is two. The standard form of a quadratic equation is ax^2 + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'x' is the variable.

The importance of writing quadratic equations in standard form lies in its utility for identifying key properties of the equation, such as the roots (solutions) and the vertex of the parabola it represents. This form also facilitates the use of various methods for solving quadratic equations, such as factoring, the quadratic formula, and graphing.

In this article, we will delve into the steps and considerations for writing a quadratic equation in standard form, exploring the benefits, common pitfalls, and practical applications of this process.

Understanding the Components of a Quadratic Equation

A quadratic equation in standard form is represented as ax^2 + bx + c = 0. Here, 'a', 'b', and 'c' are coefficients of the quadratic equation, and 'x' is the variable.

• Coefficient 'a': This is the coefficient of the x^2 term. It cannot be zero, as this would not be a quadratic equation. The value of 'a' affects the parabola's width and direction.
• Coefficient 'b': This is the coefficient of the x term. It affects the position of the parabola along the x-axis.
• Constant 'c': This is the constant term in the equation. It affects the position of the parabola along the y-axis.

Why Write in Standard Form?

Writing a quadratic equation in standard form makes it easier to identify the coefficients 'a', 'b', and 'c', which are crucial for solving the equation and analyzing the parabola it represents.

Steps to Write a Quadratic Equation in Standard Form

To write a quadratic equation in standard form, follow these steps:

1. Identify the Variable: Determine the variable in the equation. Most often, this is 'x', but it could be 'y' or any other variable depending on the context of the problem.

2. Combine Like Terms: If the equation contains multiple terms with the same variable raised to the same power, combine these terms into a single term.

3. Ensure the Coefficient of x^2 is Not Zero: If the coefficient of x^2 is zero, the equation is not quadratic and cannot be written in standard form.

4. Arrange Terms in Descending Order of Powers: Arrange the terms of the equation so that the term with the highest power of the variable comes first, followed by the term with the next highest power, and so on. For a quadratic equation, this means the x^2 term comes first, followed by the x term, and then the constant term.

5. Set the Equation Equal to Zero: To write the equation in standard form, it must be set equal to zero. If the equation is already equal to a constant, subtract that constant from both sides to set it equal to zero.

Example

Consider the equation x^2 + 5x - 2 = 0. This is already in standard form, with 'a = 1', 'b = 5', and 'c = -2'.

For an equation that is not in standard form, such as 2 + 3x^2 - x, we would first identify the variable (x in this case), then rearrange the terms in descending order of powers: 3x^2 - x + 2. Finally, we notice this equation is not equal to zero, so we would subtract 2 from both sides to set it equal to zero: 3x^2 - x = -2. Rearranging, we get 3x^2 - x + 2 = 0, which is in standard form.

Applications of Writing Quadratic Equations in Standard Form

Writing quadratic equations in standard form is essential for various applications, including:

• Solving Quadratic Equations: The standard form is crucial for applying methods like factoring, completing the square, and using the quadratic formula to find the roots of the equation.
• Graphing Parabolas: The coefficients 'a', 'b', and 'c' in the standard form provide key information about the parabola's shape, position, and vertex, making it easier to graph.
• Analyzing Physical Systems: Quadratic equations model many real-world phenomena, such as the trajectory of projectiles, the shape of reflective surfaces, and the growth of populations. Writing these equations in standard form facilitates analysis and prediction.

Common Pitfalls

One common mistake is forgetting to set the equation equal to zero. Always ensure that your final step in writing the equation in standard form is to have it equal to zero.

Another pitfall is incorrectly identifying the coefficients 'a', 'b', and 'c'. Double-check that you have correctly identified the coefficients by looking at the powers of the variable in each term.

Conclusion and Future Steps

Writing quadratic equations in standard form is a foundational skill in algebra, offering a clear pathway to solving these equations and understanding the parabolas they represent. By mastering this skill, you not only enhance your problem-solving capabilities in mathematics but also develop a deeper understanding of the real-world phenomena modeled by quadratic equations.

We hope this comprehensive guide has been informative and helpful. Now, take your first step into the fascinating world of quadratic equations. Practice converting different equations into standard form and explore the various applications and solutions of quadratic equations.