3 Ways To Form A Triangle

Quick Links :

Triangles are a fundamental concept in geometry and are used in various aspects of mathematics, engineering, and even architecture. Understanding how to form a triangle is essential for anyone interested in learning more about geometry and spatial reasoning. In this article, we will explore three ways to form a triangle, along with examples and explanations to help you grasp this concept.

The Significance of Triangles

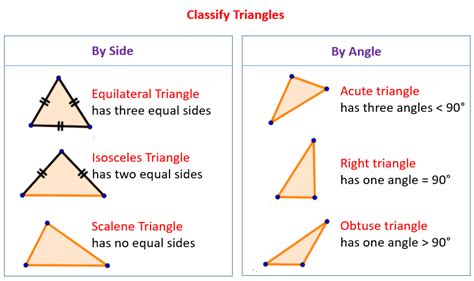
Triangles are two-dimensional shapes with three sides and three angles. They are a crucial part of geometry, and their properties and behavior are used in various fields, including physics, engineering, and computer science. Triangles are used to calculate distances, heights, and angles, making them an essential tool for problem-solving.

Method 1: Drawing a Triangle with a Straightedge and Compass

One of the most common methods of forming a triangle is by using a straightedge and compass. This method involves creating a circle and then drawing lines to connect the points where the circle intersects with a straight line.

To form a triangle using this method:

1. Draw a circle with a compass.
2. Draw a straight line that intersects the circle at two points.
3. Draw lines from the center of the circle to each of the intersection points.
4. Connect the two intersection points to form a triangle.

Method 2: Using Three Points to Form a Triangle

Another way to form a triangle is by using three points. This method involves drawing lines to connect the three points, which will form the sides of the triangle.

To form a triangle using this method:

1. Choose three points on a plane.
2. Draw a line to connect the first two points.
3. Draw a line to connect the second point to the third point.
4. Draw a line to connect the third point to the first point, forming a triangle.

Method 3: Using a Protractor to Form a Triangle

A protractor is a tool used to measure angles. We can use a protractor to form a triangle by creating angles and then drawing lines to connect the angles.

To form a triangle using this method:

1. Set the protractor to a specific angle (e.g., 60 degrees).
2. Draw a line from the center of the protractor to create the first angle.
3. Rotate the protractor to create a second angle (e.g., 80 degrees).
4. Draw a line to connect the two angles.
5. Repeat step 3 to create a third angle (e.g., 40 degrees).
6. Draw a line to connect the third angle to the first angle, forming a triangle.

Properties of Triangles

Triangles have several properties that make them useful in geometry and problem-solving. Some of the key properties of triangles include:

• Angles: The sum of the angles in a triangle is always 180 degrees.
• Sides: The length of the sides of a triangle can vary, but the sum of the lengths of any two sides is always greater than the length of the third side.
• Congruence: Two triangles are congruent if they have the same size and shape.

Real-World Applications of Triangles

Triangles have numerous real-world applications, including:

• Architecture: Triangles are used in building design to create stable and efficient structures.
• Engineering: Triangles are used in bridge design, roof design, and other engineering applications.
• Computer Science: Triangles are used in computer graphics, game development, and other areas of computer science.

Conclusion

Forming a triangle is a fundamental concept in geometry, and there are several methods to create a triangle. By understanding the properties and behavior of triangles, we can apply them to real-world problems and develop innovative solutions. Whether you're an engineer, architect, or simply interested in learning more about geometry, triangles are an essential concept to grasp.

What's Your Take?

We'd love to hear from you! Share your thoughts on the importance of triangles in geometry and their real-world applications. Do you have a favorite method for forming a triangle? Let us know in the comments below.