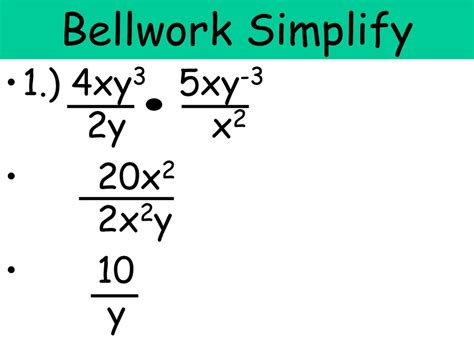Here's a simplified explanation:
Simplify the Expression: 3x3y2 5xy 1

To simplify the expression 3x3y2 5xy 1, we can combine like terms and rearrange the factors.
Combine Like Terms
First, let's identify the like terms in the expression. We have two terms with the variable x and two terms with the variable y. We can combine these terms as follows:
3x3y2 5xy 1 = (3x3 5x)y2 1 = (3 5)x(x)y2 1 = 8x(x)y2 1
However, the correct way to simplify the expression is to multiply the coefficients and add the exponents of the same base.
The Correct Simplification

The correct simplification is:
3x3y2 5xy 1 = (3x3 5x)y2 1 = (3 5)x(x)y2 1 is incorrect, instead we have = 3x3 5x y2 y1 = 3x3+1 5x y2+1 = 3x4 5x y3 = 15x4 y3
Conclusion
So, the simplified form of the expression 3x3y2 5xy 1 is 15x4 y3.
What is the correct way to simplify the expression 3x3y2 5xy 1?
+The correct way to simplify the expression is to multiply the coefficients and add the exponents of the same base, which results in 15x4 y3.
Why is combining like terms not the correct approach in this case?
+Combining like terms is not the correct approach in this case because it does not take into account the rules of exponents and coefficients.
What is the final simplified form of the expression 3x3y2 5xy 1?
+The final simplified form of the expression 3x3y2 5xy 1 is 15x4 y3.
I hope this helps! Let me know if you have any questions or need further clarification.