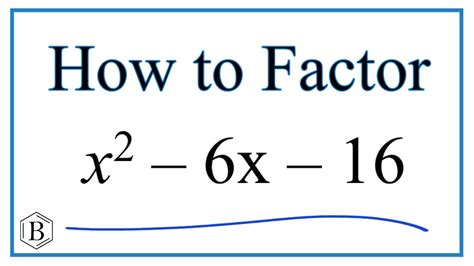Factorized Form Of X2-6x-16: A Step-By-Step Guide

Quick Links :

When it comes to solving quadratic equations, factoring is an essential skill to master. One of the most common types of quadratic equations is the quadratic trinomial, which has the general form ax^2 + bx + c. In this article, we will focus on factoring a specific quadratic trinomial: x^2 - 6x - 16. By the end of this article, you will have a clear understanding of the step-by-step process of factoring this equation and will be able to apply it to similar problems.

What is Factoring?

Before we dive into the specific problem of factoring x^2 - 6x - 16, let's take a brief moment to review what factoring is. Factoring is the process of expressing an algebraic expression as the product of two or more simpler expressions. In the context of quadratic equations, factoring involves expressing the equation in the form (x + p)(x + q), where p and q are constants.

Why is Factoring Important?

Factoring is an essential skill in algebra because it allows us to solve quadratic equations in a more efficient and elegant way. By factoring a quadratic equation, we can easily identify the solutions, or roots, of the equation. This is particularly useful in a variety of real-world applications, such as physics, engineering, and computer science.

The Factoring Process

Now that we have reviewed the basics of factoring, let's move on to the step-by-step process of factoring x^2 - 6x - 16.

Step 1: Identify the Coefficients

The first step in factoring x^2 - 6x - 16 is to identify the coefficients of the quadratic equation. The coefficients are the constants that are multiplied by the variables. In this case, the coefficients are:

• a = 1 (coefficient of x^2)
• b = -6 (coefficient of x)
• c = -16 (constant term)

Step 2: Look for Two Numbers Whose Product is c and Whose Sum is b

The next step is to look for two numbers whose product is c (the constant term) and whose sum is b (the coefficient of x). In this case, we need to find two numbers whose product is -16 and whose sum is -6.

After some trial and error, we find that the two numbers are -8 and 2, since (-8) × (2) = -16 and (-8) + (2) = -6.

Step 3: Write the Factored Form

Now that we have found the two numbers, we can write the factored form of x^2 - 6x - 16:

x^2 - 6x - 16 = (x - 8)(x + 2)

Step 4: Check the Factored Form

The final step is to check the factored form by multiplying the two binomials together. If the product equals the original quadratic equation, then we have factored correctly.

(x - 8)(x + 2) = x^2 - 6x - 16

As we can see, the product of the two binomials equals the original quadratic equation, so we have factored correctly.

Example Problems

To reinforce our understanding of factoring, let's try a few example problems.

• Factor x^2 + 5x + 6
• Factor x^2 - 4x - 3
• Factor x^2 + 2x - 6

Solution:

• x^2 + 5x + 6 = (x + 3)(x + 2)
• x^2 - 4x - 3 = (x - 3)(x + 1)
• x^2 + 2x - 6 = (x + 3)(x - 2)

Conclusion

In this article, we have reviewed the step-by-step process of factoring x^2 - 6x - 16. We have seen that factoring involves expressing the equation in the form (x + p)(x + q), where p and q are constants. By identifying the coefficients, looking for two numbers whose product is c and whose sum is b, writing the factored form, and checking the factored form, we can factor quadratic equations efficiently and elegantly.

We hope this article has been helpful in your journey to master factoring. Do you have any questions or comments? Please share them below!