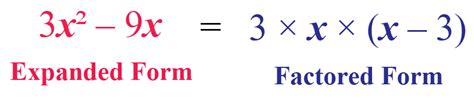Algebraic expressions are a fundamental concept in mathematics, and understanding how to factor them is crucial for solving equations, graphing functions, and analyzing mathematical models. In this article, we will delve into the world of factored forms of algebraic expressions, exploring their importance, types, and techniques for factoring.

What are Factored Forms of Algebraic Expressions?
Factored forms of algebraic expressions are a way of expressing mathematical expressions as a product of simpler expressions, called factors. Factoring involves breaking down an algebraic expression into its constituent parts, making it easier to analyze, simplify, and solve equations.
Why are Factored Forms Important?
Factored forms of algebraic expressions are essential in mathematics and science, as they:
- Simplify complex expressions, making them easier to understand and work with
- Facilitate the solution of equations and inequalities
- Enable the analysis of mathematical models and relationships
- Provide a powerful tool for graphing functions and understanding their behavior
Types of Factored Forms
There are several types of factored forms, including:
Greatest Common Factor (GCF) Factoring
GCF factoring involves finding the greatest common factor of two or more terms in an expression and factoring it out. For example:
2x + 6 = 2(x + 3)
In this example, the GCF of 2x and 6 is 2, which is factored out.

Difference of Squares Factoring
Difference of squares factoring involves factoring expressions of the form a^2 - b^2. For example:
x^2 - 4 = (x + 2)(x - 2)
In this example, the expression x^2 - 4 is factored into the product of two binomials.

Sum and Difference Factoring
Sum and difference factoring involves factoring expressions of the form a^2 + b^2 and a^2 - b^2. For example:
x^2 + 4 = (x + 2i)(x - 2i)
In this example, the expression x^2 + 4 is factored into the product of two complex binomials.

Techniques for Factoring
Several techniques can be used to factor algebraic expressions, including:
Factoring by Grouping
Factoring by grouping involves grouping terms in an expression and factoring out common factors. For example:
x^2 + 2x + 3 = (x + 1)(x + 3)
In this example, the terms x^2 and 2x are grouped, and the common factor (x + 1) is factored out.

Factoring Quadratic Expressions
Factoring quadratic expressions involves factoring expressions of the form ax^2 + bx + c. For example:
x^2 + 5x + 6 = (x + 2)(x + 3)
In this example, the quadratic expression x^2 + 5x + 6 is factored into the product of two binomials.

Conclusion
In conclusion, factored forms of algebraic expressions are a powerful tool for simplifying complex expressions, solving equations, and analyzing mathematical models. Understanding the different types of factored forms and techniques for factoring is essential for success in mathematics and science. By mastering factoring, you can unlock the secrets of algebra and take your mathematical skills to the next level.
We encourage you to share your thoughts and experiences with factoring in the comments section below. How do you use factoring in your mathematical endeavors?
What is factoring in algebra?
+Factoring in algebra involves breaking down an algebraic expression into its constituent parts, making it easier to analyze, simplify, and solve equations.
What are the different types of factored forms?
+The different types of factored forms include GCF factoring, difference of squares factoring, sum and difference factoring, and factoring quadratic expressions.
How do I factor a quadratic expression?
+To factor a quadratic expression, you can use the factoring by grouping technique or the quadratic formula.