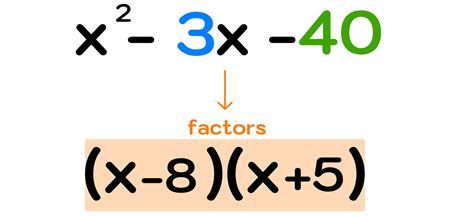Polynomials are a fundamental concept in algebra, and factoring them is a crucial skill to master. Factoring a polynomial involves expressing it as a product of simpler polynomials, known as factors. This process can be challenging, but with the right strategies, you can factor even the most complex polynomials. In this article, we will explore five ways to factor a polynomial, providing you with a comprehensive guide to improve your math skills.
Understanding Polynomials
Before we dive into factoring polynomials, let's briefly review what they are. A polynomial is an expression consisting of variables and coefficients combined using addition, subtraction, and multiplication. Polynomials can be classified into different types, such as linear, quadratic, cubic, and so on, based on the degree of the variable.
Why Factor Polynomials?
Factoring polynomials is essential in various areas of mathematics, including algebra, geometry, and calculus. Factoring helps to:
- Simplify complex expressions
- Solve equations and inequalities
- Graph functions
- Find the roots of a polynomial
- Understand the behavior of a function
5 Ways to Factor a Polynomial
Now, let's explore the five ways to factor a polynomial.
1. Greatest Common Factor (GCF) Method
The GCF method involves finding the greatest common factor of the terms in the polynomial. This method is useful when the polynomial has a common factor among all its terms.

To factor a polynomial using the GCF method:
- Find the greatest common factor of the terms.
- Divide each term by the GCF.
- Write the result as a product of the GCF and the resulting terms.
Example: Factor 6x + 12
- Find the GCF: 6
- Divide each term by 6: x + 2
- Write the result: 6(x + 2)
2. Difference of Squares Method
The difference of squares method involves factoring a polynomial that can be written as the difference of two squares.

To factor a polynomial using the difference of squares method:
- Identify the polynomial as the difference of two squares.
- Write the polynomial as (a - b)(a + b), where a and b are the square roots of the terms.
Example: Factor x^2 - 9
- Identify the polynomial as the difference of two squares.
- Write the polynomial as (x - 3)(x + 3)
3. Sum and Difference Method
The sum and difference method involves factoring a polynomial that can be written as the sum or difference of two cubes.

To factor a polynomial using the sum and difference method:
- Identify the polynomial as the sum or difference of two cubes.
- Write the polynomial as (a + b)(a^2 - ab + b^2) or (a - b)(a^2 + ab + b^2), where a and b are the cube roots of the terms.
Example: Factor x^3 + 8
- Identify the polynomial as the sum of two cubes.
- Write the polynomial as (x + 2)(x^2 - 2x + 4)
4. Grouping Method
The grouping method involves factoring a polynomial by grouping terms that have common factors.

To factor a polynomial using the grouping method:
- Group the terms into pairs that have common factors.
- Factor out the common factor from each pair.
- Write the result as a product of the common factors and the resulting terms.
Example: Factor x^3 + 2x^2 - 3x - 6
- Group the terms: (x^3 + 2x^2) - (3x + 6)
- Factor out the common factor from each pair: x^2(x + 2) - 3(x + 2)
- Write the result: (x + 2)(x^2 - 3)
5. Synthetic Division Method
The synthetic division method involves factoring a polynomial using a table to divide the polynomial by a linear factor.

To factor a polynomial using the synthetic division method:
- Create a table with the coefficients of the polynomial and the linear factor.
- Perform the division, using the table to find the quotient and remainder.
- Write the result as a product of the linear factor and the quotient.
Example: Factor x^2 + 5x + 6 using synthetic division with a linear factor of x + 2
- Create the table: | | 1 | 5 | 6 | |---|---|---|---| | 2 | | 2 | 14 |
- Perform the division:
- Write the result: (x + 2)(x + 3)
Conclusion: Factoring Polynomials with Confidence
Factoring polynomials is a crucial skill in mathematics, and with the five methods outlined above, you can tackle even the most complex polynomials with confidence. Remember to always read the problem carefully, identify the type of polynomial, and choose the most suitable method to factor it. With practice and patience, you will become proficient in factoring polynomials and develop a deeper understanding of algebra.
We hope this article has helped you to improve your math skills. Share your thoughts and feedback in the comments below!
What is the greatest common factor (GCF) of a polynomial?
+The greatest common factor (GCF) of a polynomial is the largest factor that divides all the terms of the polynomial.
How do I know which factoring method to use?
+Choose the factoring method that best suits the type of polynomial you are trying to factor. For example, if the polynomial is a difference of squares, use the difference of squares method.
Can I use synthetic division to factor any polynomial?
+No, synthetic division is only used to factor polynomials that have a linear factor. If the polynomial does not have a linear factor, use another factoring method.