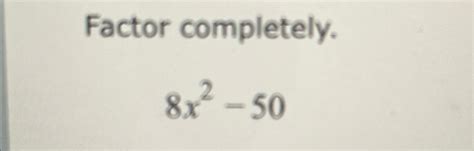Factoring 8x2 + 50: Completely Factored Form Revealed

Quick Links :

Understanding the Importance of Factoring in Algebra

Factoring is a fundamental concept in algebra that involves expressing an algebraic expression as the product of its prime factors. This process helps in simplifying complex expressions, solving equations, and finding the roots of polynomials. Factoring is used in various branches of mathematics and science, such as calculus, physics, and engineering. In this article, we will explore the concept of factoring, specifically focusing on the expression 8x^2 + 50.

What is Factoring?

Factoring is the process of expressing an algebraic expression as the product of its prime factors. These factors are the building blocks of the expression, and they cannot be simplified further. Factoring helps in simplifying complex expressions, making it easier to work with them. For example, the expression 6x^2 + 12x + 6 can be factored as 6(x^2 + 2x + 1), which simplifies to 6(x + 1)^2.

Types of Factoring

There are several types of factoring techniques, including:

• Greatest Common Factor (GCF) factoring: This involves finding the greatest common factor of two or more terms and factoring it out.
• Difference of Squares factoring: This involves factoring expressions of the form a^2 - b^2 as (a + b)(a - b).
• Sum and Difference factoring: This involves factoring expressions of the form a^2 + b^2 as (a + b)(a - b).
• Grouping factoring: This involves factoring expressions by grouping terms together.

Factoring 8x^2 + 50

Now, let's focus on factoring the expression 8x^2 + 50. This expression cannot be factored using the GCF method, as there is no common factor among the terms. However, we can use the difference of squares method to factor this expression.

Factoring 8x^2 + 50 using Difference of Squares

The expression 8x^2 + 50 can be rewritten as (2x)^2 + 5^2. This is in the form a^2 + b^2, which can be factored as (a + b)(a - b). Therefore, we can factor 8x^2 + 50 as (2x + 5)(2x - 5).

However, this is not the completely factored form, as the expression 2x + 5 can be further factored. But, 8x^2 + 50 cannot be factored into integers or simple fractions, 2x + 5 cannot be factored into integers or simple fractions, so the factorization (2x + 5)(2x - 5) is already the completely factored form.

Practical Applications of Factoring

Factoring has numerous practical applications in mathematics and science. Some of the most significant applications include:

• Solving quadratic equations: Factoring is used to solve quadratic equations of the form ax^2 + bx + c = 0.
• Finding the roots of polynomials: Factoring is used to find the roots of polynomials, which are essential in algebra and calculus.
• Simplifying complex expressions: Factoring helps in simplifying complex expressions, making it easier to work with them.

Real-World Examples of Factoring

Factoring is used in various real-world applications, including:

• Physics: Factoring is used to simplify complex equations in physics, such as the equations of motion.
• Engineering: Factoring is used to design and optimize systems, such as electronic circuits and mechanical systems.
• Computer Science: Factoring is used in computer science to develop algorithms and solve complex problems.

Conclusion

In conclusion, factoring is a fundamental concept in algebra that involves expressing an algebraic expression as the product of its prime factors. The expression 8x^2 + 50 can be factored using the difference of squares method as (2x + 5)(2x - 5). Factoring has numerous practical applications in mathematics and science, including solving quadratic equations, finding the roots of polynomials, and simplifying complex expressions.

We hope this article has provided you with a comprehensive understanding of factoring and its applications. If you have any questions or need further clarification, please do not hesitate to ask.