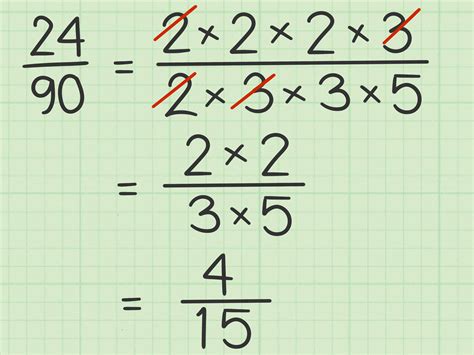Simplifying fractions is an essential math skill that can make calculations easier and more manageable. In this article, we will explore two methods to simplify the fraction 16:24.
Simplifying fractions involves reducing them to their lowest terms, where the numerator and denominator have no common factors other than 1. This makes the fraction easier to work with and understand. In the case of the fraction 16:24, we will use two methods to simplify it: the greatest common divisor (GCD) method and the prime factorization method.
Why Simplify Fractions?
Before we dive into the methods, let's quickly discuss why simplifying fractions is important. Simplifying fractions helps:
- Reduce errors in calculations
- Make calculations easier and faster
- Improve understanding of mathematical concepts
- Enhance problem-solving skills
Method 1: Greatest Common Divisor (GCD) Method
The GCD method involves finding the greatest common divisor of the numerator and denominator and dividing both numbers by the GCD.
Find the Greatest Common Divisor
To find the GCD of 16 and 24, we need to list the factors of each number.
- Factors of 16: 1, 2, 4, 8, 16
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
The greatest common divisor of 16 and 24 is 8.

Simplify the Fraction
Now that we have found the GCD, we can simplify the fraction by dividing both numbers by 8.
16 ÷ 8 = 2 24 ÷ 8 = 3
So, the simplified fraction is 2:3.
Example: Simplifying a Fraction with GCD
Simplify the fraction 12:18 using the GCD method.
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
The GCD of 12 and 18 is 6. Divide both numbers by 6.
12 ÷ 6 = 2 18 ÷ 6 = 3
The simplified fraction is 2:3.
Method 2: Prime Factorization Method
The prime factorization method involves breaking down the numerator and denominator into their prime factors and canceling out any common factors.
Prime Factorization of 16 and 24
To simplify the fraction 16:24 using the prime factorization method, we need to break down 16 and 24 into their prime factors.
- Prime factorization of 16: 2 × 2 × 2 × 2
- Prime factorization of 24: 2 × 2 × 2 × 3

Cancel Out Common Factors
Now that we have broken down 16 and 24 into their prime factors, we can cancel out any common factors.
- Cancel out three 2's: 2 × 2 × 2 × 2 = 2 × 2 × 2 × 1
- Cancel out three 2's: 2 × 2 × 2 × 3 = 2 × 2 × 1 × 3
So, the simplified fraction is 2:3.
Example: Simplifying a Fraction with Prime Factorization
Simplify the fraction 18:24 using the prime factorization method.
- Prime factorization of 18: 2 × 3 × 3
- Prime factorization of 24: 2 × 2 × 2 × 3
Cancel out common factors.
- Cancel out one 2: 2 × 3 × 3 = 1 × 3 × 3
- Cancel out one 3: 2 × 2 × 2 × 3 = 2 × 2 × 2 × 1
The simplified fraction is 3:4.
Comparison of Methods
Both the GCD method and the prime factorization method can be used to simplify fractions. However, the GCD method is often faster and more straightforward, while the prime factorization method provides a deeper understanding of the underlying mathematical structure.
Conclusion: Simplifying Fractions
Simplifying fractions is an essential math skill that can make calculations easier and more manageable. By using either the GCD method or the prime factorization method, you can simplify fractions and improve your understanding of mathematical concepts.
What is the purpose of simplifying fractions?
+Simplifying fractions helps reduce errors in calculations, makes calculations easier and faster, improves understanding of mathematical concepts, and enhances problem-solving skills.
What are the two methods to simplify fractions discussed in this article?
+The two methods to simplify fractions discussed in this article are the greatest common divisor (GCD) method and the prime factorization method.
Which method is often faster and more straightforward?
+The GCD method is often faster and more straightforward.
We hope this article has helped you understand the importance of simplifying fractions and provided you with two methods to simplify fractions. Do you have any favorite methods for simplifying fractions? Share your thoughts in the comments below!