Transformational Forms Of A Parabola Explained

Quick Links :

The parabola is a fundamental concept in mathematics, particularly in algebra and geometry. It is a U-shaped curve that can be found in various real-world applications, from the trajectory of projectiles to the design of satellite dishes. However, did you know that parabolas can be transformed into different forms, each with its unique properties and uses? In this article, we will delve into the world of transformational forms of a parabola, exploring their characteristics, equations, and practical applications.

What is a Parabola?

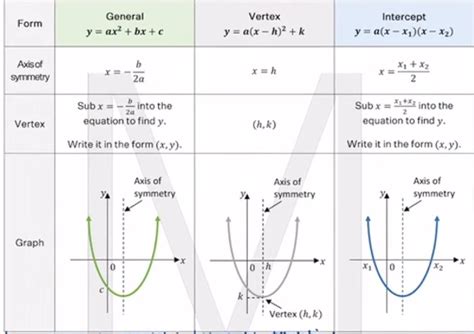
Before we dive into the transformational forms of a parabola, let's first understand what a parabola is. A parabola is a quadratic curve that is U-shaped and symmetrical about its axis. It is defined by the equation y = ax^2 + bx + c, where a, b, and c are constants. The parabola opens upwards or downwards, depending on the value of a.

Vertical and Horizontal Shifts

One of the simplest transformations of a parabola is a vertical or horizontal shift. A vertical shift occurs when the parabola is moved up or down by a certain amount, while a horizontal shift occurs when the parabola is moved left or right. These shifts can be achieved by adding or subtracting a constant value from the equation of the parabola.

For example, if we have the equation y = x^2 + 2x + 1, we can shift it vertically by 2 units by adding 2 to the equation, resulting in y = x^2 + 2x + 3. Similarly, we can shift it horizontally by 1 unit to the left by subtracting 1 from the x-value, resulting in y = (x + 1)^2 + 2(x + 1) + 1.

Equations for Vertical and Horizontal Shifts

• Vertical shift: y = ax^2 + bx + c + k
• Horizontal shift: y = a(x - h)^2 + b(x - h) + c

where k is the vertical shift and h is the horizontal shift.

Scaling and Reflection

Another type of transformation is scaling and reflection. Scaling occurs when the parabola is stretched or compressed vertically or horizontally, while reflection occurs when the parabola is flipped over the x-axis or y-axis.

Scaling can be achieved by multiplying the equation of the parabola by a constant value, while reflection can be achieved by negating the equation. For example, if we have the equation y = x^2 + 2x + 1, we can scale it vertically by 2 by multiplying the equation by 2, resulting in y = 2x^2 + 4x + 2. Similarly, we can reflect it over the x-axis by negating the equation, resulting in y = -x^2 - 2x - 1.

Equations for Scaling and Reflection

• Vertical scaling: y = a(kx^2 + bx + c)
• Horizontal scaling: y = ak^2(x^2 + bx + c)
• Reflection over x-axis: y = -ax^2 - bx - c
• Reflection over y-axis: y = a(-x)^2 + b(-x) + c

where k is the scaling factor.

Rotation

A more complex transformation is rotation, where the parabola is rotated by a certain angle around its vertex. This can be achieved by using the rotation matrix, which is a mathematical tool used to rotate points and curves.

For example, if we have the equation y = x^2 + 2x + 1, we can rotate it by 30 degrees counterclockwise by using the rotation matrix, resulting in a new equation.

Equation for Rotation

• Rotation by angle θ: x' = xcosθ - ysinθ, y' = xsinθ + ycosθ

where (x', y') are the new coordinates after rotation.

Real-World Applications

Transformational forms of a parabola have numerous real-world applications, from architecture to engineering. For example, the design of satellite dishes and telescopes relies on the use of parabolic shapes to focus signals and light. Additionally, the trajectory of projectiles, such as rockets and missiles, can be modeled using parabolic curves.

In architecture, parabolic shapes are used in the design of bridges, arches, and domes. For example, the iconic Gateway Arch in St. Louis, Missouri, is a parabolic shape that is both aesthetically pleasing and structurally sound.

Conclusion

In conclusion, transformational forms of a parabola are a fundamental concept in mathematics and have numerous real-world applications. By understanding the different types of transformations, such as vertical and horizontal shifts, scaling and reflection, and rotation, we can better appreciate the beauty and complexity of parabolic curves.

We hope this article has provided you with a deeper understanding of transformational forms of a parabola and their applications. Whether you are a student, teacher, or simply a curious learner, we encourage you to explore the fascinating world of parabolas and discover their many wonders.