5 Easy Steps To Convert Standard To Vertex Form

Quick Links :

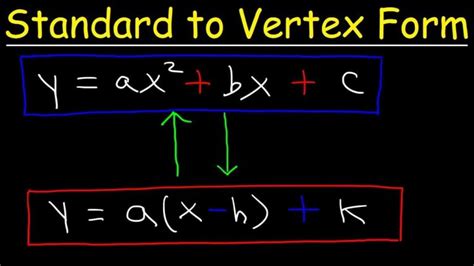
Converting a standard quadratic equation to vertex form can be a challenging task for many students, but with the right approach, it can be simplified into a manageable process. In this article, we will explore the concept of vertex form, its significance, and provide a step-by-step guide on how to convert a standard quadratic equation to vertex form.

Understanding Vertex Form

Vertex form is a way of expressing a quadratic equation in the form of f(x) = a(x - h)^2 + k, where (h, k) represents the vertex of the parabola. This form is particularly useful in identifying the key features of a parabola, such as its vertex, axis of symmetry, and maximum or minimum value.

Why Convert to Vertex Form?

Converting a standard quadratic equation to vertex form offers several benefits. It allows us to easily identify the vertex of the parabola, which is essential in graphing and analyzing quadratic functions. Additionally, vertex form makes it simpler to determine the axis of symmetry, maximum or minimum value, and the direction of the parabola's opening.

Step 1: Identify the Coefficients of the Quadratic Equation

To convert a standard quadratic equation to vertex form, we need to identify the coefficients of the quadratic equation. The standard form of a quadratic equation is f(x) = ax^2 + bx + c, where a, b, and c are constants. We need to determine the values of a, b, and c to proceed with the conversion.

Example:

Suppose we have the quadratic equation f(x) = 2x^2 + 5x + 3. In this case, a = 2, b = 5, and c = 3.

Step 2: Complete the Square

The next step is to complete the square. To do this, we need to manipulate the equation to create a perfect square trinomial. We can achieve this by adding and subtracting a constant term inside the parentheses.

Example:

Using the quadratic equation from Step 1, we can complete the square as follows:

f(x) = 2x^2 + 5x + 3 f(x) = 2(x^2 + 5/2x) + 3 f(x) = 2(x^2 + 5/2x + 25/16) - 25/8 + 3 f(x) = 2(x + 5/4)^2 - 25/8 + 3

Step 3: Simplify the Expression

Now that we have completed the square, we can simplify the expression to obtain the vertex form of the quadratic equation.

Example:

Continuing from Step 2, we can simplify the expression as follows:

f(x) = 2(x + 5/4)^2 - 25/8 + 3 f(x) = 2(x + 5/4)^2 - 25/8 + 24/8 f(x) = 2(x + 5/4)^2 - 1/8

Step 4: Identify the Vertex

With the vertex form of the quadratic equation, we can easily identify the vertex of the parabola. The vertex is represented by the coordinates (h, k), where h is the x-coordinate and k is the y-coordinate.

Example:

From Step 3, we can identify the vertex as follows:

h = -5/4 k = -1/8

The vertex is (-5/4, -1/8).

Step 5: Write the Vertex Form

Finally, we can write the vertex form of the quadratic equation by substituting the values of h and k into the standard vertex form.

Example:

Using the values of h and k from Step 4, we can write the vertex form as follows:

f(x) = 2(x - (-5/4))^2 - 1/8 f(x) = 2(x + 5/4)^2 - 1/8

We have successfully converted the standard quadratic equation to vertex form.

Now that you have learned the 5 easy steps to convert a standard quadratic equation to vertex form, you can apply this knowledge to solve a wide range of problems in mathematics and science. Remember to practice regularly to reinforce your understanding of this concept. Share your thoughts and questions in the comments section below, and don't forget to share this article with your friends and classmates who may benefit from it.