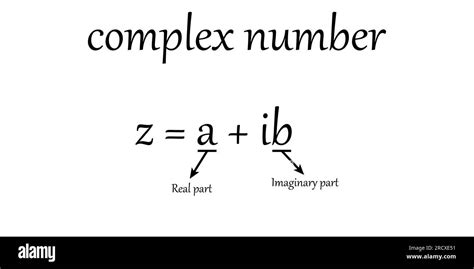When it comes to mathematics, complex numbers are often considered one of the most challenging topics to grasp. However, understanding complex numbers is crucial for various mathematical and scientific applications, such as algebra, geometry, trigonometry, and even physics and engineering. In this article, we will delve into the world of complex numbers, specifically focusing on the standard form A+Bi, and provide you with a comprehensive guide on how to simplify complex numbers with ease.
The importance of complex numbers lies in their ability to extend the real number system to the complex plane, allowing us to solve equations that cannot be solved using only real numbers. Complex numbers have numerous applications in various fields, including signal processing, control theory, and quantum mechanics. Despite their importance, complex numbers can be intimidating, especially when it comes to simplifying them. In this article, we will break down the standard form A+Bi and provide you with practical examples and step-by-step instructions on how to simplify complex numbers.

Understanding the Standard Form A+Bi
The standard form of a complex number is represented as A+Bi, where:
- A is the real part of the complex number
- B is the imaginary part of the complex number
- i is the imaginary unit, which is defined as the square root of -1
In this form, A and B are real numbers, and i is the imaginary unit that satisfies the equation i^2 = -1. The real part A and the imaginary part B can be any real numbers, including integers, fractions, and decimals.
Components of a Complex Number
A complex number in standard form has two components: the real part and the imaginary part.
- The real part A represents the x-coordinate of the complex number on the complex plane.
- The imaginary part B represents the y-coordinate of the complex number on the complex plane.
Understanding the components of a complex number is crucial for simplifying and performing operations on complex numbers.

Simplifying Complex Numbers
Simplifying complex numbers involves combining the real and imaginary parts to obtain a simpler expression. Here are some step-by-step instructions on how to simplify complex numbers:
Step 1: Combine Like Terms
Combine the real parts and the imaginary parts separately.
Example: Simplify the complex number 2+3i + 4+2i
Combine the real parts: 2 + 4 = 6 Combine the imaginary parts: 3i + 2i = 5i
The simplified complex number is 6+5i.
Step 2: Simplify Fractions
Simplify any fractions in the real or imaginary parts.
Example: Simplify the complex number 1/2 + 3/4i
Simplify the fraction in the real part: 1/2 = 0.5 Simplify the fraction in the imaginary part: 3/4 = 0.75
The simplified complex number is 0.5 + 0.75i.
Step 3: Eliminate Zero Terms
Eliminate any zero terms in the real or imaginary parts.
Example: Simplify the complex number 2+0i + 3+4i
Eliminate the zero term in the imaginary part: 0i = 0
The simplified complex number is 2 + 3 + 4i = 5+4i.

Practical Examples
Here are some practical examples of simplifying complex numbers:
- Simplify the complex number 3+2i + 2+5i
Combine the real parts: 3 + 2 = 5 Combine the imaginary parts: 2i + 5i = 7i
The simplified complex number is 5+7i.
- Simplify the complex number 1/3 + 2/5i
Simplify the fraction in the real part: 1/3 = 0.33 Simplify the fraction in the imaginary part: 2/5 = 0.4
The simplified complex number is 0.33 + 0.4i.
Common Mistakes
When simplifying complex numbers, here are some common mistakes to avoid:
- Forgetting to combine like terms
- Failing to simplify fractions
- Not eliminating zero terms
- Incorrectly handling the imaginary unit i
By avoiding these common mistakes, you can simplify complex numbers with ease and confidence.

Conclusion
Simplifying complex numbers is an essential skill in mathematics and science. By understanding the standard form A+Bi and following the step-by-step instructions outlined in this article, you can simplify complex numbers with ease. Remember to combine like terms, simplify fractions, and eliminate zero terms to obtain a simpler expression. With practice and patience, you can master the art of simplifying complex numbers and tackle even the most challenging mathematical problems.
We hope this article has helped you understand the standard form A+Bi and how to simplify complex numbers. Share your thoughts and comments below, and don't forget to like and share this article with your friends and colleagues.
What is the standard form of a complex number?
+The standard form of a complex number is A+Bi, where A is the real part and B is the imaginary part.
How do I simplify complex numbers?
+To simplify complex numbers, combine like terms, simplify fractions, and eliminate zero terms.
What are some common mistakes when simplifying complex numbers?
+Common mistakes include forgetting to combine like terms, failing to simplify fractions, not eliminating zero terms, and incorrectly handling the imaginary unit i.