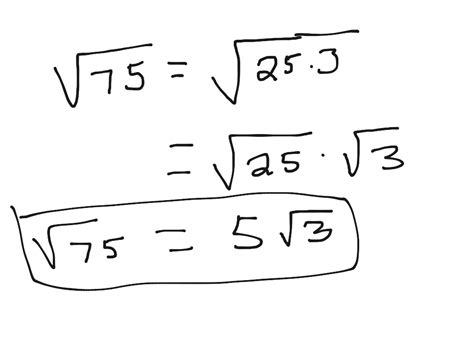Simplify The Square Root Of 75 In 3 Easy Steps

Quick Links :

The concept of simplifying square roots may seem daunting at first, but with the right approach, it can be broken down into manageable steps. In this article, we'll explore the simplification of the square root of 75 in three easy steps. Whether you're a student looking to improve your math skills or an individual seeking to refresh your knowledge, this guide is designed to provide a clear and concise explanation.

Step 1: Factorize the Number

The first step in simplifying the square root of 75 is to factorize the number. This involves breaking down 75 into its prime factors. To do this, we can start by finding the prime factors of 75. The prime factorization of 75 is:

75 = 3 × 5 × 5

Now that we have the prime factors, we can identify the perfect squares within the factorization.

Step 2: Identify Perfect Squares

The next step is to identify the perfect squares within the prime factorization. In this case, we have two identical factors of 5, which can be combined to form a perfect square:

75 = 3 × (5 × 5) = 3 × 5^2

Now that we've identified the perfect square, we can simplify the square root.

Step 3: Simplify the Square Root

The final step is to simplify the square root. Using the property of square roots that states √(ab) = √a × √b, we can rewrite the square root of 75 as:

√75 = √(3 × 5^2) = √3 × √(5^2) = √3 × 5

Therefore, the simplified form of the square root of 75 is 5√3.

In conclusion, simplifying the square root of 75 can be achieved in three easy steps: factorize the number, identify perfect squares, and simplify the square root. By following these steps, you can break down complex square roots into manageable components and arrive at a simplified solution.

Now that you've learned how to simplify the square root of 75, take a moment to practice and reinforce your understanding. Try simplifying other square roots using the same steps, and don't hesitate to reach out if you have any questions or need further clarification.