Simplify Square Root Of 63 In Radical Form

Quick Links :

The concept of square roots and radicals is a fundamental aspect of mathematics, especially in algebra and geometry. Simplifying square roots in radical form is a crucial skill that can help you solve complex mathematical problems with ease.

Understanding Square Roots and Radicals

Before diving into simplifying the square root of 63, let's first understand what square roots and radicals are. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16. Radicals, on the other hand, are a way to represent square roots using mathematical symbols.

What is a Radical?

A radical is a symbol used to represent the square root of a number. It consists of a horizontal line with a "√" symbol above it. The number under the radical sign is called the radicand. For instance, the radical form of the square root of 16 is √16.

Simplifying Square Roots in Radical Form

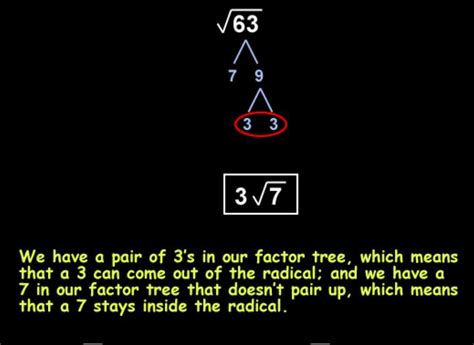
Simplifying square roots in radical form involves factoring the radicand into prime numbers and then taking out any pairs of identical prime factors. Here's how to simplify the square root of 63:

1. Factor 63 into prime numbers: 63 = 3 × 3 × 7
2. Identify pairs of identical prime factors: 3 × 3
3. Take out the pair of 3s: √(3 × 3 × 7) = 3√7

Therefore, the simplified radical form of the square root of 63 is 3√7.

Benefits of Simplifying Square Roots in Radical Form

Simplifying square roots in radical form has several benefits:

• Easier calculations: Simplifying radicals makes it easier to perform calculations involving square roots. • Improved accuracy: Simplifying radicals helps reduce errors that can occur when working with complex square root expressions. • Better understanding: Simplifying radicals helps you understand the underlying structure of the numbers involved.

Real-World Applications of Simplifying Square Roots in Radical Form

Simplifying square roots in radical form has numerous real-world applications:

• Geometry: Simplifying radicals is essential in geometry, particularly when dealing with right triangles and the Pythagorean theorem. • Physics: Simplifying radicals is crucial in physics, especially when working with equations involving distance, time, and velocity. • Engineering: Simplifying radicals is vital in engineering, particularly in fields like mechanical engineering, electrical engineering, and civil engineering.

Common Mistakes to Avoid When Simplifying Square Roots in Radical Form

When simplifying square roots in radical form, here are some common mistakes to avoid:

• Not factoring the radicand: Failing to factor the radicand into prime numbers can lead to incorrect simplification. • Not identifying pairs of identical prime factors: Overlooking pairs of identical prime factors can result in incomplete simplification. • Not taking out pairs of identical prime factors: Failing to take out pairs of identical prime factors can lead to incorrect simplification.

Conclusion: Simplifying the Square Root of 63 in Radical Form

In conclusion, simplifying the square root of 63 in radical form involves factoring the radicand into prime numbers, identifying pairs of identical prime factors, and taking out those pairs. By doing so, we can simplify the square root of 63 to 3√7. This skill is essential in mathematics, particularly in algebra and geometry, and has numerous real-world applications.

Take Action: Practice Simplifying Square Roots in Radical Form

To improve your skills in simplifying square roots in radical form, practice with different numbers and expressions. Start with simple examples and gradually move on to more complex ones. With practice and patience, you'll become proficient in simplifying square roots in radical form and be able to tackle more challenging mathematical problems.

We'd love to hear from you! Share your thoughts, questions, or comments below.