Simplify Square Roots In 1 Easy Way

Quick Links :

Simplifying square roots can seem like a daunting task, but with a few simple steps, you can master this mathematical operation. Whether you're a student looking to improve your math skills or just someone who wants to brush up on their algebra, this article will show you how to simplify square roots in a straightforward and easy way.

Mathematics is a fundamental subject that plays a crucial role in various aspects of our lives. From science and technology to finance and engineering, math is an essential tool that helps us solve problems and make informed decisions. One of the most important mathematical operations is the square root, which is used to find the number that, when multiplied by itself, gives a specified value. However, simplifying square roots can be a bit challenging, especially when dealing with complex numbers.

Fortunately, there is a simple way to simplify square roots that requires minimal calculations and is easy to understand. By using this method, you'll be able to simplify even the most complex square roots with ease.

Understanding Square Roots

Before we dive into the simplification method, it's essential to understand what square roots are and how they work. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16. Square roots are denoted by a radical symbol (√) and can be either positive or negative.

Types of Square Roots

There are two types of square roots: perfect and imperfect. A perfect square root is one that can be simplified to a whole number, such as √16 = 4. On the other hand, an imperfect square root cannot be simplified to a whole number, such as √2 = 1.414 (approximately).

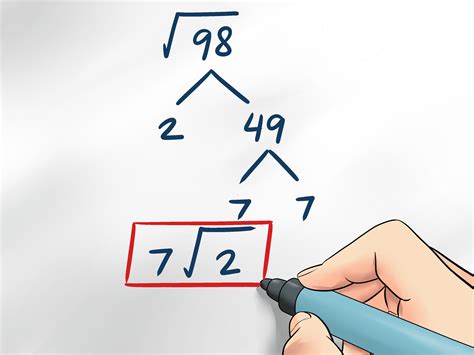
The Simplification Method

Now, let's move on to the simplification method. This method involves factoring the number under the radical symbol into its prime factors. Here's a step-by-step guide:

1. Factor the number under the radical symbol into its prime factors.
2. Look for pairs of identical prime factors.
3. Take one prime factor from each pair and multiply them together.
4. Write the result as the simplified square root.

Example: Simplifying √48

Let's use the simplification method to simplify √48.

1. Factor 48 into its prime factors: 48 = 2 × 2 × 2 × 2 × 3
2. Look for pairs of identical prime factors: 2 × 2 × 2 × 2 = (2 × 2) × (2 × 2)
3. Take one prime factor from each pair and multiply them together: 2 × 2 = 4
4. Write the result as the simplified square root: √48 = √(4 × 3) = 2√3

Benefits of Simplifying Square Roots

Simplifying square roots has several benefits, including:

• Making mathematical calculations easier and faster
• Improving accuracy and reducing errors
• Enhancing problem-solving skills and critical thinking
• Building confidence in math and problem-solving abilities

Common Mistakes to Avoid

When simplifying square roots, there are several common mistakes to avoid:

• Forgetting to factor the number under the radical symbol
• Not looking for pairs of identical prime factors
• Taking the wrong prime factors from each pair
• Not multiplying the prime factors correctly

Practical Applications of Simplifying Square Roots

Simplifying square roots has several practical applications in various fields, including:

• Physics and engineering: Simplifying square roots is essential in calculations involving velocity, acceleration, and force.
• Computer science: Square roots are used in algorithms for computer graphics, game development, and scientific simulations.
• Finance: Simplifying square roots is used in financial calculations, such as compound interest and investment returns.

Real-World Examples

Here are a few real-world examples of simplifying square roots:

• Calculating the distance between two points on a coordinate plane
• Determining the area of a circle or an ellipse
• Finding the volume of a cube or a sphere

Conclusion and Next Steps

In conclusion, simplifying square roots is an essential math skill that can be mastered with practice and patience. By using the simplification method outlined in this article, you'll be able to simplify even the most complex square roots with ease. Remember to avoid common mistakes and practice regularly to build your confidence and skills.

If you have any questions or comments, please feel free to share them in the section below. We'd love to hear from you!

FAQ Section: