Simplifying square roots is a fundamental concept in mathematics, particularly in algebra and geometry. Square roots are used to find the value of a number that, when multiplied by itself, gives a specified value. In this case, we are looking to simplify √48 in radical form.
To simplify a square root, we look for perfect square factors of the number inside the square root. A perfect square is a number that can be expressed as the product of an integer with itself. For example, 4 is a perfect square because it can be expressed as 2 × 2.
Breaking Down the Square Root of 48

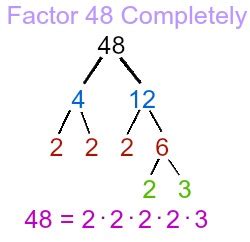
When we look at the number 48, we can break it down into its prime factors to identify any perfect square factors. The prime factorization of 48 is 2^4 × 3.
Identifying Perfect Square Factors
In the prime factorization of 48, we can see that there is a perfect square factor of 16, which is 2^4. This means that we can rewrite √48 as √(16 × 3).
Simplifying the Square Root

Using the property of square roots that allows us to separate the square root of a product into the product of square roots, we can rewrite √(16 × 3) as √16 × √3.
Evaluating the Square Root of 16
The square root of 16 is 4, since 4 × 4 = 16. Therefore, we can simplify √48 as 4√3.
Final Answer

The simplified form of √48 in radical form is 4√3.
Why Simplify Square Roots?

Simplifying square roots is important in mathematics because it allows us to work with more manageable numbers and expressions. By simplifying square roots, we can make calculations easier and more efficient. Additionally, simplifying square roots is a fundamental concept in algebra and geometry, and is used in a variety of mathematical and real-world applications.
Real-World Applications of Simplifying Square Roots

Simplifying square roots has a variety of real-world applications, including:
- Geometry: Simplifying square roots is used in geometry to find the lengths of sides of triangles and other shapes.
- Algebra: Simplifying square roots is used in algebra to solve equations and manipulate expressions.
- Physics: Simplifying square roots is used in physics to calculate distances, velocities, and other quantities.
- Engineering: Simplifying square roots is used in engineering to design and optimize systems and structures.
Conclusion

In conclusion, simplifying square roots is an important concept in mathematics that allows us to work with more manageable numbers and expressions. By simplifying square roots, we can make calculations easier and more efficient, and apply mathematical concepts to a variety of real-world situations. We hope this article has helped you to understand the concept of simplifying square roots and how to apply it to simplify √48 in radical form.
We encourage you to share your thoughts and comments on this article. Do you have any questions about simplifying square roots or its applications? Let us know in the comments section below!
What is the simplified form of √48 in radical form?
+The simplified form of √48 in radical form is 4√3.
Why is simplifying square roots important in mathematics?
+Simplifying square roots is important in mathematics because it allows us to work with more manageable numbers and expressions, making calculations easier and more efficient.
What are some real-world applications of simplifying square roots?
+Simplifying square roots has a variety of real-world applications, including geometry, algebra, physics, and engineering.