Simplify Radical 72: Break Down The Math Problem

Quick Links :

Simplifying radicals can seem intimidating, but with a clear step-by-step approach, it can be a straightforward process. In this article, we will explore the math problem of simplifying radical 72 and provide a comprehensive guide on how to break it down.

Understanding Radicals

Before diving into the problem, it's essential to understand what radicals are. A radical is a mathematical symbol used to represent the root of a number. In this case, we are dealing with the square root of 72. The radical symbol is often represented as √.

Why Simplify Radicals?

Simplifying radicals is crucial in mathematics, especially in algebra and geometry. It helps to:

• Reduce complex expressions to simpler forms
• Make calculations easier and more efficient
• Improve understanding of mathematical concepts

Breaking Down Radical 72

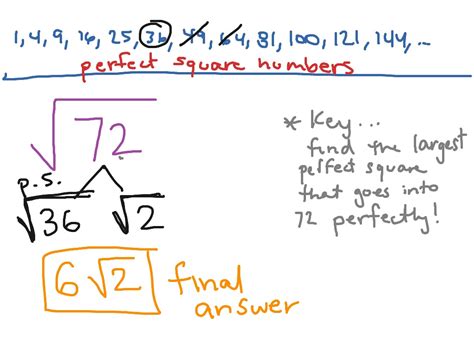
Now, let's focus on simplifying radical 72. To do this, we need to find the factors of 72 that are perfect squares.

Step 1: Find the Prime Factorization of 72

The prime factorization of 72 is: 72 = 2 × 2 × 2 × 3 × 3

Step 2: Identify Perfect Squares

We can see that 2 × 2 = 4 and 3 × 3 = 9 are perfect squares. We can rewrite 72 as: 72 = 2 × 2 × 2 × 3 × 3 = 4 × 9 × 2

Step 3: Simplify the Radical

Now, we can simplify the radical by taking the square root of the perfect squares: √72 = √(4 × 9 × 2) = √4 × √9 × √2 = 2 × 3 × √2 = 6√2

Practical Applications of Simplifying Radicals

Simplifying radicals has numerous practical applications in various fields, including:

• Geometry: Simplifying radicals helps in calculating distances, areas, and volumes of shapes.
• Algebra: Simplifying radicals is essential in solving equations and manipulating algebraic expressions.
• Physics: Simplifying radicals is used in calculating velocities, accelerations, and forces.

Real-World Examples

1. Building Design: Architects use simplified radicals to calculate the dimensions and shapes of buildings.
2. Electrical Engineering: Electrical engineers use simplified radicals to calculate the resistance and impedance of electrical circuits.
3. Computer Graphics: Computer graphics designers use simplified radicals to create 3D models and animations.

Common Mistakes to Avoid

When simplifying radicals, it's essential to avoid common mistakes, such as:

• Not checking for perfect squares
• Not simplifying the radical completely
• Not using the correct notation

Conclusion and Next Steps

Simplifying radical 72 is a straightforward process that requires attention to detail and a clear understanding of mathematical concepts. By following the steps outlined in this article, you can break down the math problem and simplify the radical with ease.

We encourage you to practice simplifying radicals and explore its practical applications in various fields. Share your thoughts and experiences in the comments section below.