Lines are fundamental elements in geometry, and understanding their properties and behaviors is crucial for problem-solving and critical thinking. One of the most important concepts in geometry is the relationship between perpendicular lines and right angles. In this article, we will delve into the world of perpendicular lines, exploring their definition, properties, and significance in geometry.
What are Perpendicular Lines?
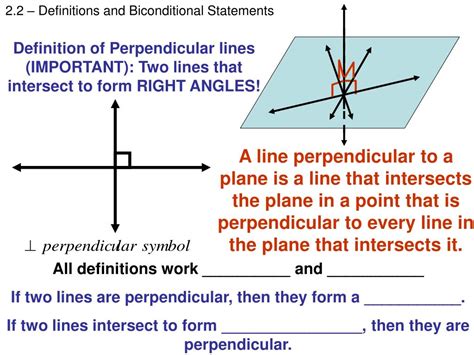
Perpendicular lines are two lines that intersect at a right angle (90 degrees). This means that the angle formed by the intersection of the two lines is equal to 90 degrees. Perpendicular lines are denoted by the symbol ⊥, which is read as "perpendicular to." For example, if we have two lines, AB and CD, and they intersect at point E, we can say that AB ⊥ CD if the angle formed by their intersection is 90 degrees.
Properties of Perpendicular Lines
Perpendicular lines have several important properties that make them useful in geometry:
- Right Angle Formation: As mentioned earlier, perpendicular lines intersect at a right angle (90 degrees). This property is essential in geometry, as it allows us to create right-angled triangles and apply trigonometric functions.
- Symmetry: Perpendicular lines have line symmetry. This means that if we reflect one line over the other, the resulting line will be identical to the original line.
- Midpoint: The point of intersection of two perpendicular lines is called the midpoint. This point is equidistant from the endpoints of both lines.
How to Determine if Two Lines are Perpendicular
To determine if two lines are perpendicular, we can use the following methods:
- Using a Protractor: Measure the angle formed by the intersection of the two lines using a protractor. If the angle is 90 degrees, then the lines are perpendicular.
- Using Coordinates: If we have the coordinates of the endpoints of both lines, we can use the slope formula to determine if the lines are perpendicular. If the product of the slopes of the two lines is -1, then the lines are perpendicular.
Real-World Applications of Perpendicular Lines
Perpendicular lines have numerous real-world applications in various fields, including:
- Architecture: Perpendicular lines are used in building design to create right-angled corners and symmetrical structures.
- Engineering: Perpendicular lines are used in engineering to design and construct bridges, roads, and other infrastructure.
- Art: Perpendicular lines are used in art to create balanced and symmetrical compositions.

Conclusion
In conclusion, perpendicular lines are an essential concept in geometry, and their properties and applications are far-reaching. By understanding the definition, properties, and significance of perpendicular lines, we can better appreciate the beauty and complexity of geometry. Whether in art, architecture, or engineering, perpendicular lines play a crucial role in creating balanced and symmetrical structures.
FAQ Section
What is the symbol for perpendicular lines?
+The symbol for perpendicular lines is ⊥, which is read as "perpendicular to."
How do we determine if two lines are perpendicular?
+We can determine if two lines are perpendicular by measuring the angle formed by their intersection using a protractor or by using the slope formula with coordinates.
What is the midpoint of two perpendicular lines?
+The midpoint of two perpendicular lines is the point of intersection, which is equidistant from the endpoints of both lines.
We hope this article has provided a comprehensive understanding of perpendicular lines and their significance in geometry. If you have any further questions or would like to explore more topics in geometry, please feel free to ask in the comments section below.