4 Key Facts About Perpendicular Lines

Quick Links :

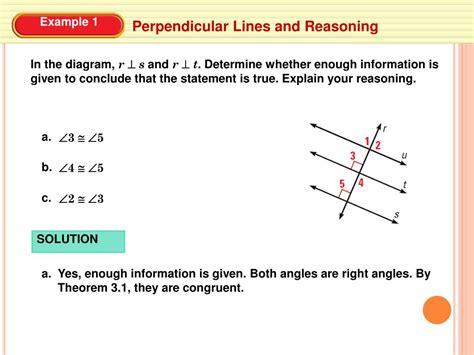
Understanding perpendicular lines is crucial in geometry and various real-world applications. These lines play a significant role in construction, architecture, and design, where precise angles and measurements are essential. In this article, we will delve into four key facts about perpendicular lines, exploring their definition, properties, and importance in different fields.

Definition and Representation

Perpendicular lines are defined as two lines that intersect at a right angle (90 degrees). This intersection is represented by the symbol ⊥. For instance, if line A intersects line B at a right angle, it can be denoted as A ⊥ B. This relationship is fundamental in understanding geometric shapes and their properties.

Properties of Perpendicular Lines

Perpendicular lines have several key properties:

• The intersection point of two perpendicular lines is called the foot of the perpendicular.
• The slopes of perpendicular lines are negative reciprocals of each other. This means that if the slope of line A is m, the slope of line B is -1/m.
• Perpendicular lines are symmetric with respect to the intersection point.

These properties are essential in solving geometric problems and proving theorems related to perpendicular lines.

Real-World Applications

Perpendicular lines have numerous real-world applications:

• Construction and Architecture: Perpendicular lines are used to ensure that buildings and bridges are constructed with precise angles and measurements, providing stability and balance.
• Design and Graphics: Perpendicular lines are used in graphic design to create visually appealing and balanced compositions.
• Physics and Engineering: Perpendicular lines are used to describe the motion of objects and the forces acting upon them, such as in the calculation of velocities and accelerations.

These applications demonstrate the importance of perpendicular lines in various fields, where accuracy and precision are crucial.

Mathematical Representations

Perpendicular lines can be represented mathematically using various methods:

• Slope-Intercept Form: The equation of a line can be written in slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept. Perpendicular lines have slopes that are negative reciprocals of each other.
• Vector Representation: Perpendicular lines can be represented using vectors, where the dot product of two vectors is zero if they are perpendicular.

These mathematical representations are essential in solving problems and proving theorems related to perpendicular lines.

Conclusion and Final Thoughts

In conclusion, perpendicular lines are a fundamental concept in geometry and have numerous real-world applications. Understanding the definition, properties, and mathematical representations of perpendicular lines is essential in various fields, including construction, design, and physics. By recognizing the importance of perpendicular lines, we can appreciate the beauty and precision of geometric shapes and their applications.

We encourage you to share your thoughts and questions about perpendicular lines in the comments section below. Your input will help us create a more engaging and informative discussion.

Actionable Steps:

1. Practice solving problems related to perpendicular lines to deepen your understanding of the concept.
2. Explore real-world applications of perpendicular lines in your field of interest.
3. Share your knowledge with others to create a community of learners.

By taking these steps, you will become more proficient in working with perpendicular lines and appreciate their significance in various aspects of life.