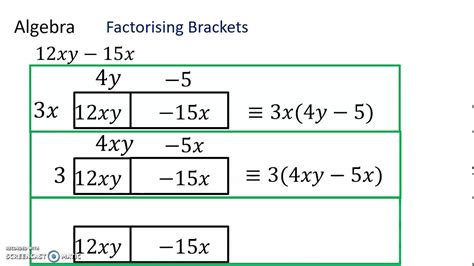
Linear Factorization Form: Simplifying Expressions

Quick Links :

Linear factorization is a crucial concept in algebra, enabling us to simplify complex expressions and equations. In this article, we will delve into the world of linear factorization, exploring its definition, benefits, and applications. By the end of this article, you will be able to understand and apply linear factorization to simplify expressions with ease.

The importance of linear factorization cannot be overstated. By breaking down complex expressions into simpler, more manageable components, we can gain a deeper understanding of the underlying mathematical structures. This, in turn, enables us to solve equations and inequalities more efficiently, making it a fundamental tool for problem-solving in mathematics and science.

So, what is linear factorization, and how does it work?

What is Linear Factorization?

Linear factorization is a process of expressing a polynomial or algebraic expression as a product of linear factors. A linear factor is a binomial expression of the form (ax + b), where a and b are constants. By factorizing an expression into linear factors, we can simplify it and make it more amenable to analysis and solution.

For example, consider the quadratic expression x^2 + 5x + 6. We can factorize this expression as (x + 3)(x + 2), where (x + 3) and (x + 2) are linear factors. This factorization simplifies the expression and makes it easier to solve equations and inequalities involving the expression.

Benefits of Linear Factorization

Linear factorization offers several benefits when working with algebraic expressions. Some of the key advantages include:

• Simplification: Linear factorization simplifies complex expressions, making them easier to analyze and solve.
• Improved understanding: By breaking down expressions into simpler components, we can gain a deeper understanding of the underlying mathematical structures.
• Efficient problem-solving: Linear factorization enables us to solve equations and inequalities more efficiently, making it a fundamental tool for problem-solving in mathematics and science.
• Enhanced algebraic manipulation: Linear factorization allows us to manipulate algebraic expressions more easily, making it easier to perform tasks such as solving systems of equations and graphing functions.

How to Factorize Linear Expressions

Factorizing linear expressions involves identifying common factors and grouping terms. Here are some steps to follow:

1. Identify common factors: Look for common factors among the terms in the expression.
2. Group terms: Group terms that have common factors together.
3. Factor out common factors: Factor out the common factors from each group of terms.
4. Simplify the expression: Simplify the resulting expression by combining like terms.

For example, consider the expression 2x^2 + 6x + 4x + 12. We can factorize this expression by identifying common factors and grouping terms:

2x^2 + 6x + 4x + 12 = 2x(x + 3) + 4(x + 3) = (2x + 4)(x + 3)

Applications of Linear Factorization

Linear factorization has numerous applications in mathematics and science. Some of the key applications include:

• Solving equations and inequalities: Linear factorization enables us to solve equations and inequalities more efficiently.
• Graphing functions: Linear factorization allows us to graph functions more easily, making it easier to visualize and analyze mathematical relationships.
• Solving systems of equations: Linear factorization enables us to solve systems of equations more efficiently, making it a fundamental tool for problem-solving in mathematics and science.

Real-World Examples of Linear Factorization

Linear factorization has numerous real-world applications. Here are a few examples:

• Computer science: Linear factorization is used in computer science to solve equations and inequalities involving complex algorithms.
• Physics: Linear factorization is used in physics to solve equations involving motion, force, and energy.
• Engineering: Linear factorization is used in engineering to solve equations involving complex systems and structures.

Conclusion

Linear factorization is a powerful tool for simplifying complex expressions and equations. By breaking down expressions into simpler components, we can gain a deeper understanding of the underlying mathematical structures and solve equations and inequalities more efficiently. With its numerous applications in mathematics and science, linear factorization is an essential technique for problem-solving and critical thinking.

We hope this article has provided you with a comprehensive understanding of linear factorization and its applications. Whether you are a student, teacher, or professional, we encourage you to share your thoughts and experiences with linear factorization in the comments section below.