Understanding the Basics of Parabolas in Vertex Form

Parabolas are a fundamental concept in algebra and geometry, and understanding how to graph them in vertex form is a crucial skill for students and professionals alike. In this article, we will explore the basics of parabolas, their importance, and five easy ways to graph them in vertex form.
A parabola is a quadratic function that can be represented in the form f(x) = ax^2 + bx + c, where a, b, and c are constants. The vertex form of a parabola is given by f(x) = a(x - h)^2 + k, where (h, k) represents the coordinates of the vertex. The vertex form is useful because it provides a clear and concise way to identify the key features of a parabola, such as its vertex, axis of symmetry, and direction of opening.
Why Graphing Parabolas in Vertex Form is Important
Graphing parabolas in vertex form is important for several reasons:
- It helps to identify the key features of a parabola, such as its vertex, axis of symmetry, and direction of opening.
- It allows us to visualize the behavior of the function and understand how it changes as x changes.
- It provides a clear and concise way to communicate mathematical ideas and solutions.
Method 1: Using the Vertex Formula

One of the easiest ways to graph a parabola in vertex form is to use the vertex formula. The vertex formula is given by (h, k) = (-b/2a, f(-b/2a)), where (h, k) represents the coordinates of the vertex.
To use the vertex formula, follow these steps:
- Identify the values of a, b, and c in the quadratic function.
- Plug the values of a and b into the vertex formula to find the x-coordinate of the vertex (h).
- Plug the value of h into the quadratic function to find the y-coordinate of the vertex (k).
- Plot the vertex on the coordinate plane.
Example: Using the Vertex Formula to Graph a Parabola
Suppose we want to graph the parabola f(x) = x^2 + 4x + 4 in vertex form. To do this, we can use the vertex formula to find the coordinates of the vertex.
First, we identify the values of a, b, and c: a = 1, b = 4, and c = 4.
Next, we plug the values of a and b into the vertex formula to find the x-coordinate of the vertex:
h = -b/2a = -4/(2*1) = -2
Then, we plug the value of h into the quadratic function to find the y-coordinate of the vertex:
k = f(-2) = (-2)^2 + 4(-2) + 4 = 4 - 8 + 4 = 0
Finally, we plot the vertex on the coordinate plane:
The vertex is (-2, 0).
Method 2: Using the Axis of Symmetry

Another way to graph a parabola in vertex form is to use the axis of symmetry. The axis of symmetry is a vertical line that passes through the vertex of the parabola.
To use the axis of symmetry, follow these steps:
- Identify the values of a, b, and c in the quadratic function.
- Find the x-coordinate of the vertex (h) using the vertex formula.
- Draw a vertical line through the vertex to represent the axis of symmetry.
- Plot the vertex on the coordinate plane.
Example: Using the Axis of Symmetry to Graph a Parabola
Suppose we want to graph the parabola f(x) = x^2 + 4x + 4 in vertex form. To do this, we can use the axis of symmetry to find the coordinates of the vertex.
First, we identify the values of a, b, and c: a = 1, b = 4, and c = 4.
Next, we find the x-coordinate of the vertex (h) using the vertex formula:
h = -b/2a = -4/(2*1) = -2
Then, we draw a vertical line through the vertex to represent the axis of symmetry:
The axis of symmetry is x = -2.
Finally, we plot the vertex on the coordinate plane:
The vertex is (-2, 0).
Method 3: Using the Vertex and a Point

Another way to graph a parabola in vertex form is to use the vertex and a point. This method involves finding the coordinates of the vertex and a point on the parabola, and then using those coordinates to graph the parabola.
To use the vertex and a point, follow these steps:
- Identify the values of a, b, and c in the quadratic function.
- Find the coordinates of the vertex (h, k) using the vertex formula.
- Find a point on the parabola by plugging a value of x into the quadratic function.
- Plot the vertex and the point on the coordinate plane.
Example: Using the Vertex and a Point to Graph a Parabola
Suppose we want to graph the parabola f(x) = x^2 + 4x + 4 in vertex form. To do this, we can use the vertex and a point to find the coordinates of the vertex.
First, we identify the values of a, b, and c: a = 1, b = 4, and c = 4.
Next, we find the coordinates of the vertex (h, k) using the vertex formula:
h = -b/2a = -4/(2*1) = -2 k = f(-2) = (-2)^2 + 4(-2) + 4 = 4 - 8 + 4 = 0
Then, we find a point on the parabola by plugging a value of x into the quadratic function. Let's say we plug in x = 0:
f(0) = 0^2 + 4(0) + 4 = 4
So, the point is (0, 4).
Finally, we plot the vertex and the point on the coordinate plane:
The vertex is (-2, 0), and the point is (0, 4).
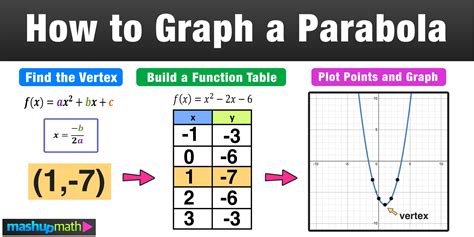
Method 4: Using a Table of Values

Another way to graph a parabola in vertex form is to use a table of values. This method involves creating a table of x and y values for the parabola, and then using those values to graph the parabola.
To use a table of values, follow these steps:
- Identify the values of a, b, and c in the quadratic function.
- Create a table of x and y values for the parabola by plugging in different values of x into the quadratic function.
- Plot the points from the table on the coordinate plane.
Example: Using a Table of Values to Graph a Parabola
Suppose we want to graph the parabola f(x) = x^2 + 4x + 4 in vertex form. To do this, we can use a table of values to find the coordinates of the vertex.
First, we identify the values of a, b, and c: a = 1, b = 4, and c = 4.
Next, we create a table of x and y values for the parabola by plugging in different values of x into the quadratic function:
| x | f(x) |
|---|---|
| -3 | 7 |
| -2 | 4 |
| -1 | 3 |
| 0 | 4 |
| 1 | 7 |
| 2 | 12 |
| 3 | 19 |
Then, we plot the points from the table on the coordinate plane:
The points are (-3, 7), (-2, 4), (-1, 3), (0, 4), (1, 7), (2, 12), and (3, 19).
Method 5: Using Graphing Software

Finally, another way to graph a parabola in vertex form is to use graphing software. This method involves using software such as Desmos or Graphing Calculator to graph the parabola.
To use graphing software, follow these steps:
- Identify the values of a, b, and c in the quadratic function.
- Enter the quadratic function into the graphing software.
- Adjust the settings as needed to graph the parabola.
Example: Using Graphing Software to Graph a Parabola
Suppose we want to graph the parabola f(x) = x^2 + 4x + 4 in vertex form. To do this, we can use graphing software to find the coordinates of the vertex.
First, we identify the values of a, b, and c: a = 1, b = 4, and c = 4.
Next, we enter the quadratic function into the graphing software:
f(x) = x^2 + 4x + 4
Then, we adjust the settings as needed to graph the parabola.
Finally, we use the graphing software to find the coordinates of the vertex:
The vertex is (-2, 0).
In conclusion, graphing parabolas in vertex form is an important skill in algebra and geometry. By using one of the five methods outlined above, you can easily graph a parabola in vertex form and identify its key features. Whether you are a student or a professional, understanding how to graph parabolas is essential for success in mathematics and science.
Now it's your turn! Try graphing a parabola using one of the methods outlined above. Share your results with a friend or classmate and discuss any challenges you encountered. Don't forget to practice, practice, practice – the more you graph parabolas, the more comfortable you will become with the process.
What is the vertex form of a parabola?
+The vertex form of a parabola is given by f(x) = a(x - h)^2 + k, where (h, k) represents the coordinates of the vertex.
How do I find the vertex of a parabola?
+To find the vertex of a parabola, you can use the vertex formula: (h, k) = (-b/2a, f(-b/2a)), where (h, k) represents the coordinates of the vertex.
What is the axis of symmetry of a parabola?
+The axis of symmetry of a parabola is a vertical line that passes through the vertex of the parabola. It is given by the equation x = h, where h is the x-coordinate of the vertex.