5 Ways To Convert Quadratic Equations To Standard Form

Quick Links :

Quadratic equations are a fundamental concept in algebra and are used to model a wide range of real-world phenomena, from the trajectory of a projectile to the growth of a population. However, quadratic equations can be complex and difficult to work with, especially when they are not in standard form. Converting a quadratic equation to standard form is an essential skill that can make it easier to solve and analyze the equation. In this article, we will explore five ways to convert quadratic equations to standard form.

What is Standard Form?

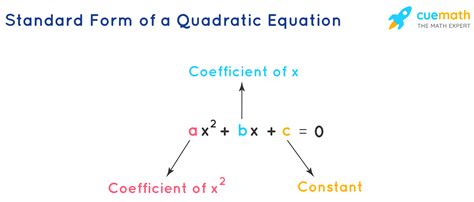
Before we dive into the methods for converting quadratic equations to standard form, let's first define what standard form is. The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable. This form is also known as the general form of a quadratic equation.

Method 1: Factoring

Factoring is a popular method for converting quadratic equations to standard form. The idea is to factor the quadratic expression into the product of two binomials. For example, consider the quadratic equation x^2 + 5x + 6 = 0. We can factor this equation as (x + 3)(x + 2) = 0. By factoring the quadratic expression, we can easily identify the values of a, b, and c in the standard form.

Steps for Factoring

• Write down the quadratic equation.
• Look for two numbers whose product is c and whose sum is b.
• Write the quadratic expression as the product of two binomials using the numbers found in step 2.
• Simplify the expression to obtain the standard form.

Method 2: Completing the Square

Completing the square is another method for converting quadratic equations to standard form. This method involves manipulating the quadratic expression to create a perfect square trinomial. For example, consider the quadratic equation x^2 + 6x + 8 = 0. We can complete the square by adding and subtracting (b/2)^2 to the expression. In this case, we add and subtract (6/2)^2 = 9 to obtain x^2 + 6x + 9 - 1 = 0. This can be simplified to (x + 3)^2 - 1 = 0, which is in standard form.

Steps for Completing the Square

• Write down the quadratic equation.
• Move the constant term to the right-hand side of the equation.
• Add and subtract (b/2)^2 to the left-hand side of the equation.
• Simplify the expression to obtain the standard form.

Method 3: Using the Quadratic Formula

The quadratic formula is a powerful tool for solving quadratic equations. We can also use it to convert quadratic equations to standard form. The quadratic formula is x = (-b ± √(b^2 - 4ac)) / 2a. By rearranging this formula, we can obtain the standard form of the quadratic equation.

Steps for Using the Quadratic Formula

• Write down the quadratic equation.
• Identify the values of a, b, and c.
• Plug these values into the quadratic formula.
• Simplify the expression to obtain the standard form.

Method 4: Using a Graphing Calculator

A graphing calculator is a useful tool for visualizing quadratic equations. We can also use it to convert quadratic equations to standard form. By graphing the quadratic equation, we can identify the x-intercepts and the vertex of the parabola. From this information, we can write down the standard form of the quadratic equation.

Steps for Using a Graphing Calculator

• Enter the quadratic equation into the graphing calculator.
• Graph the equation to identify the x-intercepts and the vertex.
• Use this information to write down the standard form of the quadratic equation.

Method 5: Using a Computer Algebra System

A computer algebra system (CAS) is a powerful tool for manipulating mathematical expressions. We can use a CAS to convert quadratic equations to standard form. By entering the quadratic equation into the CAS, we can simplify the expression and obtain the standard form.

Steps for Using a Computer Algebra System

• Enter the quadratic equation into the CAS.
• Simplify the expression to obtain the standard form.

Now that we have explored five ways to convert quadratic equations to standard form, let's summarize the key points. We can use factoring, completing the square, the quadratic formula, a graphing calculator, or a computer algebra system to convert quadratic equations to standard form. Each method has its advantages and disadvantages, and the choice of method depends on the specific quadratic equation and the individual's preference.

We hope this article has been informative and helpful. Do you have any favorite methods for converting quadratic equations to standard form? Share your thoughts in the comments below!