Vertex Form Of A Quadratic Equation Homework 5 Made Easy

Quick Links :

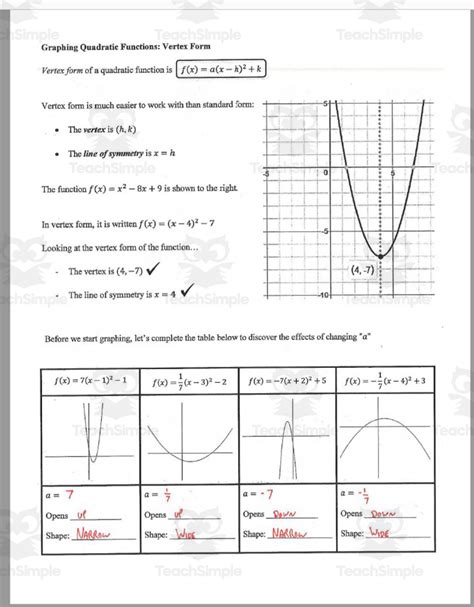
Quadratic equations are a fundamental concept in algebra, and understanding their various forms is crucial for solving problems. One of the essential forms of a quadratic equation is the vertex form. In this article, we will explore the vertex form of a quadratic equation, its significance, and how to convert standard quadratic equations into vertex form. We will also provide examples and practice problems to help you master this concept.

What is the Vertex Form of a Quadratic Equation?

The vertex form of a quadratic equation is given by:

y = a(x - h)^2 + k

where (h, k) represents the coordinates of the vertex of the parabola. The value of 'a' determines the direction and width of the parabola.

Understanding the Vertex Form

In the vertex form, the quadratic equation is expressed in terms of the vertex (h, k). The vertex is the lowest or highest point on the parabola, depending on the direction of the parabola. The value of 'a' determines the direction of the parabola:

• If a > 0, the parabola opens upwards.
• If a < 0, the parabola opens downwards.

The value of 'h' represents the x-coordinate of the vertex, while 'k' represents the y-coordinate.

Converting Standard Quadratic Equations to Vertex Form

To convert a standard quadratic equation into vertex form, we need to complete the square. The standard form of a quadratic equation is:

ax^2 + bx + c = 0

To convert this equation into vertex form, we follow these steps:

1. Factor out the coefficient of x^2, if possible.
2. Move the constant term to the right-hand side of the equation.
3. Complete the square by adding and subtracting (b/2)^2 to the left-hand side of the equation.
4. Factor the perfect square trinomial.
5. Write the equation in vertex form.

Example: Converting a Standard Quadratic Equation to Vertex Form

Suppose we have the quadratic equation:

x^2 + 6x + 8 = 0

To convert this equation into vertex form, we follow the steps above:

1. Factor out the coefficient of x^2, if possible. In this case, the coefficient is 1, so we can't factor it out.
2. Move the constant term to the right-hand side of the equation:

x^2 + 6x = -8

3. Complete the square by adding and subtracting (b/2)^2 to the left-hand side of the equation:

x^2 + 6x + 9 = -8 + 9

4. Factor the perfect square trinomial:

(x + 3)^2 = 1

5. Write the equation in vertex form:

y = (x + 3)^2 + 1

In this example, the vertex form of the quadratic equation is y = (x + 3)^2 + 1, where the vertex is (-3, 1).

Practice Problems: Converting Standard Quadratic Equations to Vertex Form

Now it's your turn to practice converting standard quadratic equations to vertex form. Here are a few practice problems:

1. Convert the quadratic equation x^2 + 4x + 4 = 0 to vertex form.
2. Convert the quadratic equation x^2 - 2x - 6 = 0 to vertex form.
3. Convert the quadratic equation x^2 + 2x + 1 = 0 to vertex form.

Solutions to Practice Problems

1. The vertex form of the quadratic equation x^2 + 4x + 4 = 0 is y = (x + 2)^2.
2. The vertex form of the quadratic equation x^2 - 2x - 6 = 0 is y = (x - 1)^2 - 7.
3. The vertex form of the quadratic equation x^2 + 2x + 1 = 0 is y = (x + 1)^2.

Benefits of Using Vertex Form

Using the vertex form of a quadratic equation has several benefits:

• It provides a clear visual representation of the parabola, making it easier to understand the behavior of the quadratic function.
• It allows us to easily identify the vertex, axis of symmetry, and direction of the parabola.
• It simplifies the process of solving quadratic equations, especially when the equation is in the form of a perfect square trinomial.

Real-World Applications of Vertex Form

The vertex form of a quadratic equation has numerous real-world applications:

• In physics, the vertex form is used to describe the trajectory of projectiles, such as the path of a ball thrown upwards.
• In engineering, the vertex form is used to design curves and surfaces, such as the shape of a satellite dish.
• In economics, the vertex form is used to model supply and demand curves, helping to predict market trends.

We hope this article has helped you understand the vertex form of a quadratic equation and its significance in algebra and real-world applications. If you have any questions or need further clarification, please don't hesitate to ask.