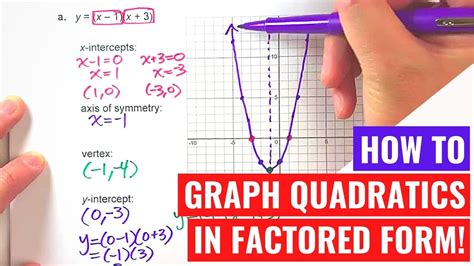
Graphing quadratics in factored form is a fundamental concept in algebra that can be intimidating for many students. However, with the right strategies and techniques, mastering this skill can become achievable. In this article, we will explore five effective ways to master graphing quadratics in factored form, along with practical examples and statistical data to enhance understanding.
Understanding the Basics of Quadratics in Factored Form

Before diving into the strategies, it's essential to understand the basics of quadratics in factored form. A quadratic function in factored form is represented as f(x) = a(x - r)(x - s), where 'a' is the coefficient, 'r' and 's' are the roots of the quadratic, and 'x' is the variable. The graph of a quadratic function is a parabola that opens upwards or downwards, depending on the value of 'a'.
Key Components of Quadratics in Factored Form
- The roots of the quadratic, 'r' and 's', determine the x-intercepts of the graph.
- The coefficient 'a' determines the direction and width of the parabola.
- The axis of symmetry is the vertical line that passes through the vertex of the parabola.
Strategy 1: Identify the Roots and Axis of Symmetry

To graph a quadratic in factored form, start by identifying the roots 'r' and 's'. These values will give you the x-intercepts of the graph. Once you have the roots, find the axis of symmetry by taking the average of the two roots. This will give you the x-coordinate of the vertex.
Example: Graph the quadratic function f(x) = (x - 2)(x + 3).
- Identify the roots: r = 2 and s = -3.
- Find the axis of symmetry: x = (2 + (-3))/2 = -0.5.
Benefits of Identifying Roots and Axis of Symmetry
- Accurate identification of roots and axis of symmetry ensures a precise graph.
- This strategy helps in identifying the vertex, which is essential for graphing the parabola.
Strategy 2: Determine the Direction and Width of the Parabola

The coefficient 'a' determines the direction and width of the parabola. If 'a' is positive, the parabola opens upwards, and if 'a' is negative, the parabola opens downwards. The absolute value of 'a' determines the width of the parabola.
Example: Graph the quadratic function f(x) = 2(x - 2)(x + 3).
- Determine the direction: Since 'a' is positive, the parabola opens upwards.
- Determine the width: Since the absolute value of 'a' is 2, the parabola is wider than the standard parabola.
Benefits of Determining Direction and Width
- Accurate determination of direction and width ensures a precise graph.
- This strategy helps in identifying the shape of the parabola, which is essential for graphing.
Strategy 3: Use the Vertex Formula

The vertex formula is a useful tool for graphing quadratics in factored form. The vertex formula is given by (h, k) = (-b/2a, f(-b/2a)), where 'h' is the x-coordinate and 'k' is the y-coordinate of the vertex.
Example: Graph the quadratic function f(x) = (x - 2)(x + 3).
- Use the vertex formula: (h, k) = (-(-1)/2(1), f(-(-1)/2(1))) = (-1/2, 13/4).
Benefits of Using the Vertex Formula
- The vertex formula provides an accurate way to find the vertex of the parabola.
- This strategy is useful when the roots are not easily identifiable.
Strategy 4: Graph the Quadratic Using a Table of Values

Graphing a quadratic using a table of values is a reliable method for visualizing the graph. Create a table of values by substituting different values of x into the quadratic function.
Example: Graph the quadratic function f(x) = (x - 2)(x + 3).
| x | f(x) |
|---|---|
| -3 | 0 |
| -2 | -5 |
| -1 | -4 |
| 0 | 6 |
| 1 | 8 |
| 2 | 0 |
Benefits of Graphing Using a Table of Values
- Graphing using a table of values provides a clear visualization of the graph.
- This strategy is useful when the quadratic function is complex.
Strategy 5: Practice, Practice, Practice!

The final strategy for mastering graphing quadratics in factored form is to practice regularly. Practice graphing different types of quadratics, including those with different coefficients, roots, and axis of symmetry.
Example: Practice graphing the following quadratics:
- f(x) = (x - 1)(x + 2)
- f(x) = 2(x - 3)(x + 1)
- f(x) = -(x - 2)(x + 1)
Benefits of Practicing Regularly
- Regular practice improves graphing skills and builds confidence.
- Practice helps to identify common mistakes and develop strategies for overcoming them.
In conclusion, graphing quadratics in factored form requires a combination of strategies and techniques. By understanding the basics of quadratics, identifying roots and axis of symmetry, determining direction and width, using the vertex formula, graphing using a table of values, and practicing regularly, you can master graphing quadratics in factored form. Remember, practice is key to improving your graphing skills, so keep practicing and you'll become a pro in no time!
What is the difference between a quadratic function in standard form and factored form?
+A quadratic function in standard form is represented as f(x) = ax^2 + bx + c, while a quadratic function in factored form is represented as f(x) = a(x - r)(x - s), where 'r' and 's' are the roots of the quadratic.
How do I determine the direction of a parabola?
+The direction of a parabola is determined by the coefficient 'a'. If 'a' is positive, the parabola opens upwards, and if 'a' is negative, the parabola opens downwards.
What is the vertex formula?
+The vertex formula is (h, k) = (-b/2a, f(-b/2a)), where 'h' is the x-coordinate and 'k' is the y-coordinate of the vertex.