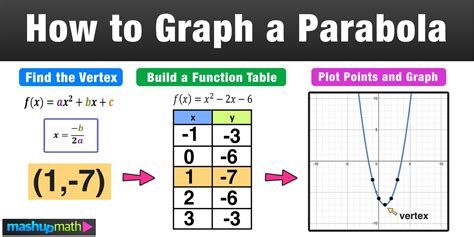
The world of quadratic equations can be a daunting one, especially when it comes to graphing. However, with the right tools and techniques, graphing quadratic equations in vertex form can become a breeze. In this article, we'll explore the ins and outs of graphing quadratic equations in vertex form, and provide you with the knowledge and skills you need to become a pro.
Graphing quadratic equations is an essential skill in algebra and mathematics, and is used in a wide range of fields, from physics and engineering to economics and computer science. By mastering the art of graphing quadratic equations, you'll be able to visualize and analyze complex relationships, and make informed decisions in a variety of contexts.
Understanding Quadratic Equations in Vertex Form

A quadratic equation in vertex form is written in the form:
f(x) = a(x - h)^2 + k
Where:
- f(x) is the quadratic function
- a is the coefficient of the quadratic term
- (x - h) is the linear term
- h is the x-coordinate of the vertex
- k is the y-coordinate of the vertex
The vertex form of a quadratic equation provides a convenient way to identify the vertex of the parabola, which is the lowest or highest point on the graph.
Benefits of Graphing Quadratic Equations in Vertex Form
Graphing quadratic equations in vertex form has several benefits, including:
- Easy identification of the vertex: The vertex form makes it easy to identify the vertex of the parabola, which is the lowest or highest point on the graph.
- Simple graphing: With the vertex form, graphing quadratic equations becomes a simple matter of plotting the vertex and using the coefficient "a" to determine the direction and width of the parabola.
- Analysis of quadratic relationships: By graphing quadratic equations in vertex form, you can analyze complex relationships between variables and make informed decisions.
Steps for Graphing Quadratic Equations in Vertex Form

Graphing quadratic equations in vertex form involves the following steps:
- Write the equation in vertex form: Rewrite the quadratic equation in the form f(x) = a(x - h)^2 + k.
- Identify the vertex: Identify the vertex of the parabola, which is the point (h, k).
- Plot the vertex: Plot the vertex on the graph.
- Determine the direction: Determine the direction of the parabola based on the coefficient "a". If a > 0, the parabola opens upward. If a < 0, the parabola opens downward.
- Determine the width: Determine the width of the parabola based on the coefficient "a". If |a| > 1, the parabola is narrow. If |a| < 1, the parabola is wide.
- Plot additional points: Plot additional points on the graph to confirm the shape and direction of the parabola.
Examples of Graphing Quadratic Equations in Vertex Form
Let's take a look at some examples of graphing quadratic equations in vertex form:
- Example 1: Graph the quadratic equation f(x) = 2(x - 3)^2 + 4.
- Example 2: Graph the quadratic equation f(x) = -(x + 2)^2 - 5.
- Example 3: Graph the quadratic equation f(x) = 0.5(x - 1)^2 - 3.
By following the steps outlined above, you can easily graph quadratic equations in vertex form and analyze complex relationships between variables.
Common Mistakes to Avoid When Graphing Quadratic Equations in Vertex Form

When graphing quadratic equations in vertex form, there are several common mistakes to avoid, including:
- Incorrect identification of the vertex: Make sure to identify the vertex correctly, as this will affect the entire graph.
- Incorrect determination of the direction: Make sure to determine the direction of the parabola correctly, based on the coefficient "a".
- Incorrect determination of the width: Make sure to determine the width of the parabola correctly, based on the coefficient "a".
- Failure to plot additional points: Make sure to plot additional points on the graph to confirm the shape and direction of the parabola.
By avoiding these common mistakes, you can ensure that your graphs are accurate and informative.
Conclusion
Graphing quadratic equations in vertex form is a valuable skill that can help you analyze complex relationships and make informed decisions. By following the steps outlined in this article, and avoiding common mistakes, you can become a pro at graphing quadratic equations in vertex form.We hope this article has been helpful in explaining the ins and outs of graphing quadratic equations in vertex form. Do you have any questions or comments? Please share them with us in the comments section below.
What is the vertex form of a quadratic equation?
+The vertex form of a quadratic equation is written in the form f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the parabola.
How do I graph a quadratic equation in vertex form?
+To graph a quadratic equation in vertex form, follow these steps: 1) Write the equation in vertex form, 2) Identify the vertex, 3) Plot the vertex, 4) Determine the direction and width, and 5) Plot additional points.
What are some common mistakes to avoid when graphing quadratic equations in vertex form?
+Common mistakes to avoid include incorrect identification of the vertex, incorrect determination of the direction and width, and failure to plot additional points.