Polynomial From Zeros And Degree Multiplicity Calculator Tool

Quick Links :

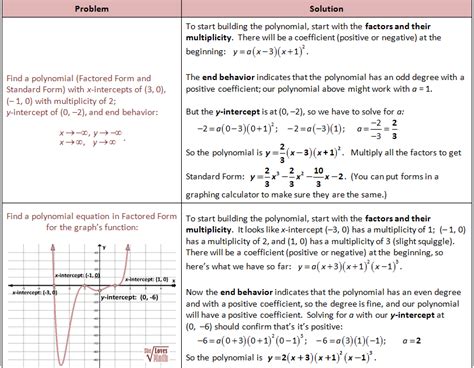
In mathematics, polynomials are expressions consisting of variables and coefficients combined using only addition, subtraction, and multiplication. They are a fundamental concept in algebra and are used to describe a wide range of phenomena in various fields, including physics, engineering, and computer science. One of the key aspects of polynomials is their zeros, which are the values of the variable that make the polynomial equal to zero. In this article, we will explore the concept of polynomial zeros and degree multiplicity, and introduce a calculator tool that can help you work with these concepts.

Polynomial zeros are crucial in understanding the behavior of polynomials, as they determine the roots of the equation. The degree of a polynomial, on the other hand, determines the maximum number of zeros it can have. However, the relationship between zeros and degree is not always straightforward, as some zeros may have multiplicity greater than one. This means that the polynomial may have repeated roots, which can affect its behavior and properties.

Understanding Polynomial Zeros

A polynomial zero is a value of the variable that makes the polynomial equal to zero. In other words, it is a root of the polynomial equation. For example, consider the polynomial x^2 + 4x + 4. By factoring, we can see that this polynomial has two zeros, x = -2 and x = -2. These zeros are also known as roots or solutions of the polynomial equation.

Polynomial zeros can be real or complex numbers, and they can be distinct or repeated. The number of zeros a polynomial has is determined by its degree, which is the highest power of the variable in the polynomial. For example, a quadratic polynomial (degree 2) can have at most two zeros, while a cubic polynomial (degree 3) can have at most three zeros.

Types of Polynomial Zeros

There are several types of polynomial zeros, including:

• Real zeros: These are zeros that are real numbers. For example, x = 2 is a real zero of the polynomial x^2 - 4.
• Complex zeros: These are zeros that are complex numbers. For example, x = 2i is a complex zero of the polynomial x^2 + 4.
• Distinct zeros: These are zeros that are distinct from each other. For example, x = 2 and x = 3 are distinct zeros of the polynomial (x - 2)(x - 3).
• Repeated zeros: These are zeros that are repeated, meaning that the polynomial has a factor of the form (x - a)^n, where n is a positive integer. For example, x = 2 is a repeated zero of the polynomial (x - 2)^2.

Understanding Degree Multiplicity

Degree multiplicity refers to the number of times a polynomial zero is repeated. In other words, it is the number of times a factor of the form (x - a) appears in the polynomial. For example, the polynomial (x - 2)^2 has degree multiplicity 2, because the factor (x - 2) appears twice.

Degree multiplicity is important because it affects the behavior of the polynomial. For example, a polynomial with repeated zeros may have a different graph than a polynomial with distinct zeros.

Calculating Degree Multiplicity

Calculating degree multiplicity can be done by factoring the polynomial and counting the number of times each factor appears. For example, the polynomial x^2 + 4x + 4 can be factored as (x + 2)^2, which means that the degree multiplicity of the zero x = -2 is 2.

Alternatively, degree multiplicity can be calculated using the derivative of the polynomial. The derivative of a polynomial is a new polynomial that represents the rate of change of the original polynomial. By taking the derivative of a polynomial and factoring it, we can determine the degree multiplicity of each zero.

Polynomial From Zeros And Degree Multiplicity Calculator Tool

The Polynomial From Zeros And Degree Multiplicity Calculator Tool is an online calculator that can help you work with polynomial zeros and degree multiplicity. This tool allows you to input a polynomial and calculate its zeros, as well as determine the degree multiplicity of each zero.

To use the calculator, simply enter the polynomial in the input field and click the "Calculate" button. The calculator will then display the zeros of the polynomial, along with their degree multiplicity.

For example, suppose we want to calculate the zeros of the polynomial x^2 + 4x + 4. We can enter this polynomial into the calculator and click the "Calculate" button. The calculator will then display the zeros of the polynomial, along with their degree multiplicity.

Benefits of Using the Calculator

Using the Polynomial From Zeros And Degree Multiplicity Calculator Tool can have several benefits, including:

• Saving time: Calculating polynomial zeros and degree multiplicity by hand can be time-consuming and tedious. The calculator can perform these calculations quickly and accurately, saving you time and effort.
• Increasing accuracy: The calculator can perform calculations with high accuracy, reducing the risk of human error.
• Enhancing understanding: By using the calculator to explore polynomial zeros and degree multiplicity, you can gain a deeper understanding of these concepts and how they relate to each other.

Conclusion

In conclusion, polynomial zeros and degree multiplicity are important concepts in algebra that can be used to understand the behavior of polynomials. The Polynomial From Zeros And Degree Multiplicity Calculator Tool is a powerful online calculator that can help you work with these concepts, saving you time and increasing accuracy. By using this tool, you can gain a deeper understanding of polynomial zeros and degree multiplicity, and explore the many applications of these concepts in mathematics and science.

We hope this article has provided you with a comprehensive introduction to polynomial zeros and degree multiplicity, and has shown you how to use the Polynomial From Zeros And Degree Multiplicity Calculator Tool to work with these concepts. If you have any questions or comments, please don't hesitate to contact us.