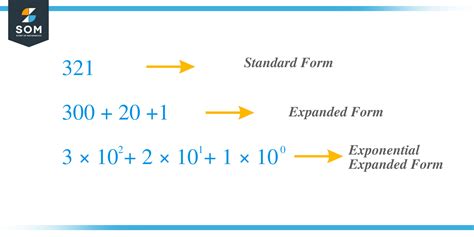
Exponential Expanded Form Made Easy

Quick Links :

Exponential notation can be a daunting concept for many students, but understanding exponential expanded form is a crucial skill for success in mathematics and science. Exponential expressions are used to represent repeated multiplication of the same number, and being able to expand these expressions is essential for simplifying and solving equations.

Understanding Exponential Notation

Exponential notation is a shorthand way of writing repeated multiplication of the same number. For example, instead of writing 2 × 2 × 2 × 2, we can write 2^4. The number 2 is called the base, and the number 4 is called the exponent. The exponent tells us how many times the base is multiplied by itself.

Why is Exponential Expanded Form Important?

Exponential expanded form is important because it allows us to simplify and solve equations that involve exponential expressions. By expanding exponential expressions, we can identify patterns and relationships between numbers, which is essential for problem-solving in mathematics and science.

How to Expand Exponential Expressions

Expanding exponential expressions is a straightforward process. Here are the steps:

1. Identify the base and exponent of the exponential expression.
2. Write the base number as many times as indicated by the exponent.
3. Multiply the base numbers together.

For example, let's expand the exponential expression 3^4:

1. Identify the base and exponent: 3 is the base, and 4 is the exponent.
2. Write the base number 3 as many times as indicated by the exponent: 3 × 3 × 3 × 3
3. Multiply the base numbers together: 3 × 3 × 3 × 3 = 81

Therefore, the expanded form of 3^4 is 81.

Examples of Exponential Expanded Form

Here are a few more examples of exponential expanded form:

• 2^3 = 2 × 2 × 2 = 8
• 4^2 = 4 × 4 = 16
• 5^1 = 5

Notice that when the exponent is 1, the exponential expression is simply equal to the base number.

Properties of Exponents

There are several properties of exponents that are important to understand:

• Product of Powers: When we multiply two exponential expressions with the same base, we add the exponents. For example, 2^3 × 2^4 = 2^(3+4) = 2^7.
• Power of a Power: When we raise an exponential expression to a power, we multiply the exponents. For example, (2^3)^4 = 2^(3×4) = 2^12.
• Power of a Product: When we raise a product of numbers to a power, we raise each number to that power. For example, (2 × 3)^4 = 2^4 × 3^4.

Understanding these properties of exponents is essential for simplifying and solving equations that involve exponential expressions.

Real-World Applications of Exponential Expanded Form

Exponential expanded form has many real-world applications, including:

• Finance: Exponential expressions are used to calculate compound interest and investment returns.
• Science: Exponential expressions are used to model population growth and chemical reactions.
• Computer Science: Exponential expressions are used in algorithms and data structures.

In conclusion, exponential expanded form is an essential skill for success in mathematics and science. By understanding how to expand exponential expressions and apply the properties of exponents, we can simplify and solve equations that involve exponential expressions. Whether you're a student or a professional, mastering exponential expanded form will help you to tackle complex problems with confidence.