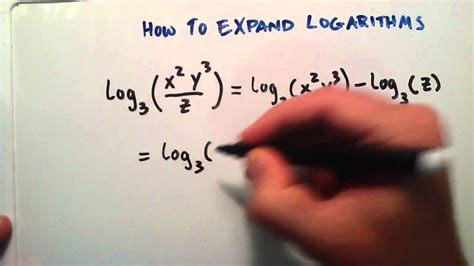Expanded form logarithms are a fundamental concept in mathematics, particularly in algebra and calculus. Understanding and mastering them can help you tackle complex problems and applications in various fields, including science, engineering, and finance. In this article, we will explore five ways to master expanded form logarithms, providing you with a comprehensive guide to improve your skills and confidence.
Understanding the Basics of Expanded Form Logarithms

Before diving into the five ways to master expanded form logarithms, it's essential to understand the basics. Expanded form logarithms represent a logarithmic expression as a sum of simpler logarithmic expressions. This form is useful for simplifying complex logarithmic expressions and making calculations more manageable.
For example, the expanded form of log(a × b) is log(a) + log(b). This property allows you to break down a logarithmic expression into smaller components, making it easier to work with.
Breaking Down Logarithmic Expressions
To master expanded form logarithms, you need to be able to break down logarithmic expressions into their simplest components. This involves using the properties of logarithms, such as the product rule, quotient rule, and power rule.
For instance, the expression log(a^2 × b^3) can be broken down using the power rule and product rule:
log(a^2 × b^3) = log(a^2) + log(b^3) = 2log(a) + 3log(b)
By breaking down logarithmic expressions, you can simplify complex problems and make calculations more efficient.
Using Logarithmic Identities

Logarithmic identities are essential for working with expanded form logarithms. These identities provide a way to simplify and manipulate logarithmic expressions, making it easier to solve problems.
Some common logarithmic identities include:
- log(a) + log(b) = log(a × b)
- log(a) - log(b) = log(a ÷ b)
- log(a^n) = nlog(a)
By applying these identities, you can simplify complex logarithmic expressions and make calculations more manageable.
Applying Logarithmic Identities to Expanded Form
When working with expanded form logarithms, you can apply logarithmic identities to simplify and manipulate the expressions. For example:
log(a × b^2) = log(a) + log(b^2) = log(a) + 2log(b)
By applying the product rule and power rule, you can simplify the expression and make calculations more efficient.
Practicing with Examples and Exercises

Practice is key to mastering expanded form logarithms. Working through examples and exercises helps you develop a deeper understanding of the concepts and builds your problem-solving skills.
Try practicing with different types of logarithmic expressions, such as:
- log(a × b)
- log(a ÷ b)
- log(a^n)
Start with simple expressions and gradually move on to more complex ones. This will help you build confidence and proficiency in working with expanded form logarithms.
Using Online Resources and Tools
There are many online resources and tools available to help you practice and master expanded form logarithms. These include:
- Online calculators and logarithmic tables
- Interactive math software and apps
- Video tutorials and lectures
Take advantage of these resources to supplement your practice and reinforce your understanding of expanded form logarithms.
Applying Expanded Form Logarithms to Real-World Problems

Expanded form logarithms have many practical applications in various fields, including science, engineering, and finance. By applying these concepts to real-world problems, you can develop a deeper understanding of their significance and relevance.
For example, expanded form logarithms are used in:
- Signal processing and audio engineering
- Data compression and coding theory
- Financial modeling and risk analysis
Try to find examples of how expanded form logarithms are used in different fields and industries. This will help you appreciate their importance and relevance.
Collaborating with Others and Seeking Feedback
Collaborating with others and seeking feedback is an essential part of mastering expanded form logarithms. Working with peers or mentors can help you:
- Identify areas for improvement
- Develop new strategies and techniques
- Refine your problem-solving skills
Don't be afraid to ask for help or seek feedback from others. This will help you grow and improve as a math student and practitioner.
Staying Motivated and Persistent

Mastering expanded form logarithms requires dedication, persistence, and motivation. It's essential to stay focused and motivated, even when faced with challenging problems or difficult concepts.
Here are some tips to help you stay motivated:
- Set achievable goals and milestones
- Celebrate your progress and successes
- Find real-world applications and examples
- Work with others and seek feedback
By staying motivated and persistent, you can overcome obstacles and achieve mastery in expanded form logarithms.
What is the expanded form of log(a × b)?
+The expanded form of log(a × b) is log(a) + log(b).
How do I simplify log(a^2 × b^3)?
+Using the power rule and product rule, log(a^2 × b^3) can be simplified to 2log(a) + 3log(b).
What are some real-world applications of expanded form logarithms?
+Expanded form logarithms have many practical applications in fields such as signal processing, data compression, and financial modeling.
By following these five ways to master expanded form logarithms, you can develop a deeper understanding of this fundamental concept and improve your skills in mathematics. Remember to stay motivated, persistent, and collaborative, and don't be afraid to seek feedback and ask for help. With practice and dedication, you can become proficient in working with expanded form logarithms and apply them to real-world problems.