In mathematics, proportions are an essential concept that helps us understand the relationship between different quantities. Ratios, on the other hand, are a way to express the comparison between two or more numbers. But do ratios form a proportion easily? Let's dive into the world of proportions and ratios to find out.
What is a Ratio?
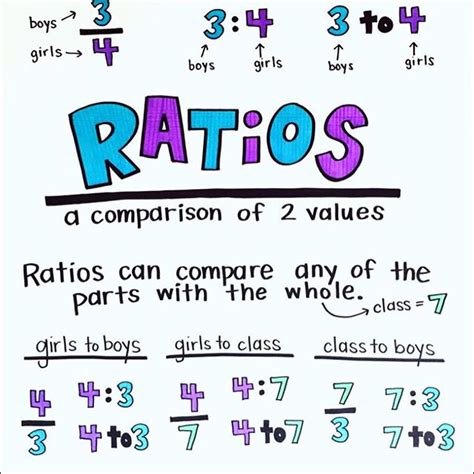
A ratio is a way to compare two or more numbers by dividing one number by the other. It is often expressed as a fraction, with a colon (:), or using the division symbol (/). For example, if we want to compare the number of apples to the number of bananas in a fruit salad, we can write the ratio as 3:4 or 3/4.
What is a Proportion?
A proportion is a statement that two ratios are equal. It is often expressed using an equals sign (=) to indicate that the two ratios are equivalent. For example, if we have two ratios, 3:4 and 6:8, we can say that they are in proportion because they have the same value when simplified.
How Do Ratios Form a Proportion?
Ratios can form a proportion when they have the same value when simplified. In other words, if two ratios can be expressed as equivalent fractions, then they are in proportion. For example, if we have two ratios, 2:3 and 4:6, we can simplify them to 2/3 and 4/6, respectively. Since 2/3 = 4/6, we can say that the two ratios are in proportion.
However, not all ratios form a proportion easily. For instance, if we have two ratios, 2:3 and 5:7, they do not form a proportion because their simplified fractions are not equal.

How to Check if Ratios Form a Proportion
To check if two ratios form a proportion, we need to simplify them to their equivalent fractions and then compare them. Here are the steps:
- Simplify each ratio to its lowest terms.
- Write the simplified fractions for each ratio.
- Compare the fractions to see if they are equal.
If the fractions are equal, then the ratios are in proportion. If they are not equal, then the ratios do not form a proportion.
Examples of Ratios Forming a Proportion
Here are some examples of ratios that form a proportion:
- 2:3 and 4:6 (both simplify to 2/3)
- 3:4 and 6:8 (both simplify to 3/4)
- 1:2 and 3:6 (both simplify to 1/2)
Examples of Ratios Not Forming a Proportion
Here are some examples of ratios that do not form a proportion:
- 2:3 and 5:7 (simplify to 2/3 and 5/7, respectively)
- 3:4 and 2:5 (simplify to 3/4 and 2/5, respectively)
- 1:2 and 3:5 (simplify to 1/2 and 3/5, respectively)
Benefits of Understanding Ratios and Proportions
Understanding ratios and proportions is essential in various aspects of life, including mathematics, science, engineering, and finance. Here are some benefits of understanding ratios and proportions:
- Problem-solving: Ratios and proportions help us solve problems involving equivalent fractions, scaling, and proportionality.
- Data analysis: Ratios and proportions help us analyze data and make informed decisions in fields like finance, economics, and science.
- Critical thinking: Understanding ratios and proportions helps us develop critical thinking skills, which are essential in making informed decisions.

Real-World Applications of Ratios and Proportions
Ratios and proportions have numerous real-world applications in various fields, including:
- Finance: Ratios and proportions are used to calculate interest rates, investment returns, and financial ratios.
- Science: Ratios and proportions are used to describe the relationships between different physical quantities, such as speed, distance, and time.
- Engineering: Ratios and proportions are used to design and optimize systems, such as bridges, buildings, and electronic circuits.
Common Mistakes When Working with Ratios and Proportions
When working with ratios and proportions, it's easy to make mistakes if you're not careful. Here are some common mistakes to avoid:
- Not simplifying ratios: Failing to simplify ratios can lead to incorrect conclusions.
- Not comparing equivalent fractions: Failing to compare equivalent fractions can lead to incorrect conclusions.
- Not checking for proportionality: Failing to check if two ratios are in proportion can lead to incorrect conclusions.

Conclusion
In conclusion, ratios can form a proportion when they have the same value when simplified. Understanding ratios and proportions is essential in various aspects of life, including mathematics, science, engineering, and finance. By avoiding common mistakes and applying ratios and proportions in real-world applications, we can make informed decisions and solve problems more effectively.
Share Your Thoughts!
We hope this article has helped you understand ratios and proportions better. Do you have any questions or examples you'd like to share? Please leave a comment below, and we'll be happy to help!
What is the difference between a ratio and a proportion?
+A ratio is a comparison between two or more numbers, while a proportion is a statement that two ratios are equal.
How do I check if two ratios form a proportion?
+To check if two ratios form a proportion, simplify each ratio to its lowest terms, write the simplified fractions, and compare them. If the fractions are equal, then the ratios are in proportion.
What are some real-world applications of ratios and proportions?
+Ratios and proportions have numerous real-world applications in fields like finance, science, engineering, and more.