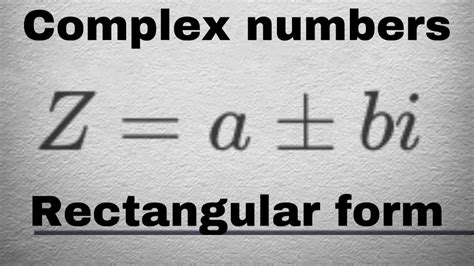Complex Numbers In Rectangular Form Explained

Quick Links :

In the realm of mathematics, complex numbers are a fundamental concept that has far-reaching implications in various fields, including physics, engineering, and computer science. At the heart of complex numbers lies the rectangular form, a representation that simplifies the manipulation and understanding of these intricate entities. In this article, we will delve into the world of complex numbers in rectangular form, exploring their importance, benefits, and practical applications.

What are Complex Numbers?

Complex numbers are an extension of the real number system, consisting of a real part and an imaginary part. They can be expressed in the form a + bi, where 'a' is the real part, 'b' is the imaginary part, and 'i' is the imaginary unit, satisfying i^2 = -1. This seemingly abstract concept has a wide range of applications in mathematics, science, and engineering.

Rectangular Form of Complex Numbers

The rectangular form, also known as the Cartesian form, represents complex numbers as points on a coordinate plane. The x-axis represents the real part, while the y-axis represents the imaginary part. This form is particularly useful for performing arithmetic operations, such as addition and multiplication, on complex numbers.

Benefits of Rectangular Form

• Simplifies arithmetic operations: The rectangular form makes it easier to perform arithmetic operations on complex numbers, such as addition, subtraction, multiplication, and division.
• Provides a visual representation: The coordinate plane representation allows for a visual understanding of complex numbers, making it easier to comprehend their properties and behavior.
• Facilitates the use of trigonometry: The rectangular form is closely related to trigonometry, enabling the use of trigonometric functions to manipulate and analyze complex numbers.

Working with Rectangular Form

To work with complex numbers in rectangular form, follow these steps:

1. Add and subtract complex numbers: Add or subtract the real parts and imaginary parts separately.
2. Multiply complex numbers: Multiply the real parts and imaginary parts, and then combine the results.
3. Divide complex numbers: Multiply the numerator and denominator by the conjugate of the denominator, and then simplify.

Practical Applications of Rectangular Form

• Electrical engineering: Complex numbers in rectangular form are used to analyze and design electrical circuits, particularly in the context of AC circuits.
• Signal processing: The rectangular form is used to represent and manipulate signals in signal processing, enabling the use of techniques such as filtering and modulation.
• Navigation and control systems: Complex numbers in rectangular form are used in navigation and control systems to represent positions, velocities, and accelerations.

Common Operations with Rectangular Form

Some common operations performed on complex numbers in rectangular form include:

• Conjugation: Finding the conjugate of a complex number by changing the sign of the imaginary part.
• Modulus: Calculating the magnitude or modulus of a complex number using the Pythagorean theorem.
• Argument: Finding the argument or angle of a complex number using trigonometric functions.

Statistical Data and Examples

• Euler's formula: The rectangular form is closely related to Euler's formula, which states that e^(ix) = cos(x) + i*sin(x).
• Complex exponential function: The rectangular form is used to represent the complex exponential function, which is essential in many mathematical and scientific applications.

Real-World Applications of Rectangular Form

The rectangular form of complex numbers has numerous real-world applications, including:

• Medical imaging: Complex numbers in rectangular form are used in medical imaging techniques such as MRI and CT scans.
• Image processing: The rectangular form is used in image processing to represent and manipulate images.
• Control systems: Complex numbers in rectangular form are used in control systems to design and analyze control systems.

Conclusion and Future Directions

In conclusion, complex numbers in rectangular form are a fundamental concept in mathematics and science, with numerous applications in various fields. By understanding the benefits and practical applications of rectangular form, we can harness the power of complex numbers to solve complex problems and make new discoveries.

As we move forward, the importance of complex numbers in rectangular form will only continue to grow, driving innovation and progress in fields such as physics, engineering, and computer science.

We invite you to share your thoughts and experiences with complex numbers in rectangular form. How have you used this concept in your studies or profession? What challenges have you faced, and how have you overcome them? Share your insights and help us build a community of learners and practitioners who are passionate about complex numbers and their applications.