Alternative Forms Of The Derivative Explained Simply

Quick Links :

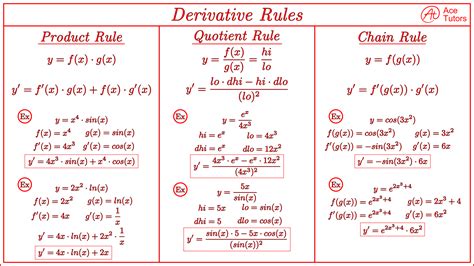
The concept of a derivative is a fundamental idea in calculus, and it has numerous applications in various fields, including physics, engineering, and economics. In essence, a derivative measures how a function changes as its input changes. However, the traditional definition of a derivative can be intimidating, especially for beginners. Fortunately, there are alternative forms of the derivative that can simplify our understanding and calculation of derivatives.

Derivatives are used to analyze functions and understand their behavior, which is crucial in many real-world applications. For instance, in physics, derivatives are used to calculate the velocity and acceleration of objects. In economics, derivatives are used to model the behavior of markets and understand the impact of changes in variables such as interest rates and prices. Despite its importance, the traditional definition of a derivative can be complex and difficult to understand.

The traditional definition of a derivative is based on the concept of limits, which can be challenging to grasp for many students. This is where alternative forms of the derivative come in. These alternative forms provide a simpler and more intuitive way of understanding and calculating derivatives.

What are Alternative Forms of the Derivative?

Alternative forms of the derivative refer to different ways of representing and calculating derivatives. These alternative forms can be used to simplify the calculation of derivatives and provide a deeper understanding of the concept. Some common alternative forms of the derivative include the geometric definition, the rate of change definition, and the infinitesimal definition.

Geometric Definition of the Derivative

The geometric definition of the derivative is based on the idea of slope. The derivative of a function at a point represents the slope of the tangent line to the graph of the function at that point. This definition provides a visual and intuitive way of understanding derivatives.

The geometric definition of the derivative can be represented mathematically as:

f'(x) = lim(h → 0) [f(x + h) - f(x)]/h

This definition is useful for understanding the concept of derivatives and visualizing the behavior of functions.

Rate of Change Definition of the Derivative

The rate of change definition of the derivative is based on the idea of measuring the rate at which a function changes as its input changes. This definition provides a practical and intuitive way of understanding derivatives.

The rate of change definition of the derivative can be represented mathematically as:

f'(x) = lim(h → 0) [f(x + h) - f(x)]/h

This definition is useful for understanding the concept of derivatives and modeling real-world phenomena.

Infinitesimal Definition of the Derivative

The infinitesimal definition of the derivative is based on the idea of infinitesimal changes in the input and output of a function. This definition provides a mathematical and rigorous way of understanding derivatives.

The infinitesimal definition of the derivative can be represented mathematically as:

f'(x) = lim(Δx → 0) [f(x + Δx) - f(x)]/Δx

This definition is useful for understanding the concept of derivatives and developing mathematical models.

Benefits of Alternative Forms of the Derivative

Alternative forms of the derivative provide several benefits, including:

• Simplified calculation of derivatives
• Deeper understanding of the concept of derivatives
• Visual and intuitive representation of derivatives
• Practical and intuitive way of modeling real-world phenomena

These benefits make alternative forms of the derivative an essential tool for students and professionals in various fields.

Real-World Applications of Alternative Forms of the Derivative

Alternative forms of the derivative have numerous real-world applications, including:

• Physics: Alternative forms of the derivative are used to calculate the velocity and acceleration of objects.
• Engineering: Alternative forms of the derivative are used to design and optimize systems.
• Economics: Alternative forms of the derivative are used to model the behavior of markets and understand the impact of changes in variables.

These applications demonstrate the importance and relevance of alternative forms of the derivative.

Conclusion

In conclusion, alternative forms of the derivative provide a simplified and intuitive way of understanding and calculating derivatives. These alternative forms have numerous real-world applications and provide a deeper understanding of the concept of derivatives. By understanding and applying alternative forms of the derivative, students and professionals can develop a stronger foundation in calculus and improve their problem-solving skills.

We invite you to share your thoughts and experiences with alternative forms of the derivative in the comments section below. How have you applied alternative forms of the derivative in your studies or profession? What benefits have you experienced from using alternative forms of the derivative?