Calculate Vectors In Minutes: 5 Easy Steps

Quick Links :

Understanding Vectors and Their Importance in Various Fields

Vectors are a fundamental concept in mathematics and physics, and their applications are diverse and widespread. From physics and engineering to computer graphics and game development, vectors play a crucial role in describing and analyzing various phenomena. Despite their importance, many students and professionals find it challenging to work with vectors, especially when it comes to calculations. However, with the right approach and techniques, calculating vectors can be a breeze.

In this article, we will explore the basics of vectors, their significance in different fields, and provide a step-by-step guide on how to calculate vectors in minutes. Whether you're a student looking to improve your math skills or a professional seeking to enhance your problem-solving abilities, this article will provide you with the necessary knowledge and tools to work with vectors confidently.

What Are Vectors?

A vector is a mathematical object that has both magnitude (length) and direction. It can be represented graphically as an arrow in a coordinate system, with the length of the arrow representing the magnitude and the direction of the arrow representing the direction of the vector. Vectors can be used to represent various physical quantities, such as displacement, velocity, acceleration, and force.

Vectors are commonly denoted by a bold letter, such as a or F, and can be represented in different forms, including:

• Component form: A vector can be represented as a sum of its components along the x, y, and z axes. For example, a vector a can be represented as a = (a1, a2, a3).
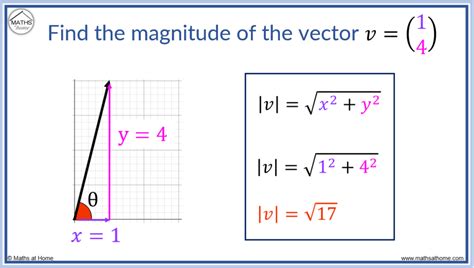
• Magnitude and direction: A vector can be represented by its magnitude (length) and direction. For example, a vector a can be represented as a = (|a|, θ), where |a| is the magnitude and θ is the direction.

Types of Vectors

There are several types of vectors, including:

• Unit vectors: Vectors with a magnitude of 1, often used to represent directions.
• Zero vectors: Vectors with a magnitude of 0, often used to represent the absence of a quantity.
• Position vectors: Vectors that represent the position of a point in space.

Why Are Vectors Important?

Vectors are essential in various fields, including:

• Physics and engineering: Vectors are used to describe and analyze various physical phenomena, such as motion, forces, and energies.
• Computer graphics: Vectors are used to represent 3D models and perform transformations, such as rotations and translations.
• Game development: Vectors are used to represent game objects and perform calculations, such as collision detection and physics simulations.

5 Easy Steps to Calculate Vectors in Minutes

Calculating vectors can be a straightforward process if you follow these 5 easy steps:

Step 1: Identify the Type of Vector Calculation

Determine the type of vector calculation you need to perform, such as finding the magnitude, direction, or component of a vector.

Step 2: Write Down the Given Information

Write down the given information, such as the components of the vector, its magnitude, or direction.

Step 3: Choose the Right Formula

Choose the right formula to use for the calculation, such as the formula for finding the magnitude of a vector or the formula for finding the component of a vector.

Step 4: Plug in the Values and Calculate

Plug in the values into the formula and perform the calculation.

Step 5: Simplify and Write Down the Final Answer

Simplify the result and write down the final answer.

Example: Calculating the Magnitude of a Vector

Suppose we have a vector a = (3, 4, 5) and we want to find its magnitude. We can use the formula:

|a| = √(a1^2 + a2^2 + a3^2)

Plugging in the values, we get:

|a| = √(3^2 + 4^2 + 5^2) |a| = √(9 + 16 + 25) |a| = √50 |a| ≈ 7.07

Therefore, the magnitude of the vector a is approximately 7.07.

Conclusion

Calculating vectors can be a straightforward process if you follow the right steps and use the right formulas. By understanding the basics of vectors and their importance in various fields, you can develop a strong foundation for working with vectors. Whether you're a student or a professional, mastering vector calculations can help you solve problems more efficiently and effectively.