8 Ways To Master Multiplying Binomials Form G

Quick Links :

Multiplying binomials is a fundamental concept in algebra that can be a bit tricky to grasp at first, but with practice and the right strategies, it can become second nature. In this article, we will explore eight ways to master multiplying binomials, focusing on the FOIL method and other techniques to help you become a pro at multiplying binomials.

Understanding the FOIL Method

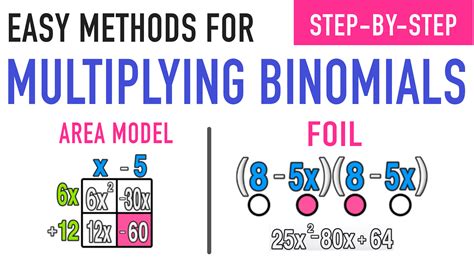
The FOIL method is a widely used technique for multiplying binomials. FOIL stands for First, Outer, Inner, Last, which refers to the order in which you multiply the terms. To use the FOIL method, follow these steps:

• Multiply the first terms of each binomial (First)
• Multiply the outer terms of each binomial (Outer)
• Multiply the inner terms of each binomial (Inner)
• Multiply the last terms of each binomial (Last)
• Add up all the terms to get the final product

Example: (x + 3)(x + 5)

Using the FOIL method, we get:

• First: x*x = x^2
• Outer: x*5 = 5x
• Inner: 3*x = 3x
• Last: 3*5 = 15
• Adding up all the terms: x^2 + 5x + 3x + 15 = x^2 + 8x + 15

Using the Box Method

The box method is another technique for multiplying binomials. To use the box method, draw a box with four quadrants and multiply the terms as follows:

• Top-left quadrant: Multiply the first terms of each binomial
• Top-right quadrant: Multiply the outer terms of each binomial
• Bottom-left quadrant: Multiply the inner terms of each binomial
• Bottom-right quadrant: Multiply the last terms of each binomial
• Add up all the terms to get the final product

Example: (x + 3)(x + 5)

Using the box method, we get:

• Top-left quadrant: x*x = x^2
• Top-right quadrant: x*5 = 5x
• Bottom-left quadrant: 3*x = 3x
• Bottom-right quadrant: 3*5 = 15
• Adding up all the terms: x^2 + 5x + 3x + 15 = x^2 + 8x + 15

Using the Distributive Property

The distributive property is a fundamental concept in algebra that can be used to multiply binomials. To use the distributive property, multiply each term in the first binomial by each term in the second binomial.

Example: (x + 3)(x + 5)

Using the distributive property, we get:

• x*(x + 5) = x^2 + 5x
• 3*(x + 5) = 3x + 15
• Adding up all the terms: x^2 + 5x + 3x + 15 = x^2 + 8x + 15

Using the Grid Method

The grid method is a visual technique for multiplying binomials. To use the grid method, draw a grid with four quadrants and multiply the terms as follows:

• Top-left quadrant: Multiply the first terms of each binomial
• Top-right quadrant: Multiply the outer terms of each binomial
• Bottom-left quadrant: Multiply the inner terms of each binomial
• Bottom-right quadrant: Multiply the last terms of each binomial
• Add up all the terms to get the final product

Example: (x + 3)(x + 5)

Using the grid method, we get:

• Top-left quadrant: x*x = x^2
• Top-right quadrant: x*5 = 5x
• Bottom-left quadrant: 3*x = 3x
• Bottom-right quadrant: 3*5 = 15
• Adding up all the terms: x^2 + 5x + 3x + 15 = x^2 + 8x + 15

Using Algebra Tiles

Algebra tiles are a hands-on tool for multiplying binomials. To use algebra tiles, represent each term in the binomial as a tile and multiply the tiles as follows:

• Multiply the first terms of each binomial
• Multiply the outer terms of each binomial
• Multiply the inner terms of each binomial
• Multiply the last terms of each binomial
• Add up all the tiles to get the final product

Example: (x + 3)(x + 5)

Using algebra tiles, we get:

• x*x = x^2
• x*5 = 5x
• 3*x = 3x
• 3*5 = 15
• Adding up all the tiles: x^2 + 5x + 3x + 15 = x^2 + 8x + 15

Using Online Tools

There are many online tools available that can help you multiply binomials. Some popular options include:

• Mathway
• Wolfram Alpha
• Symbolab
• Microsoft Math Solver

These tools can help you visualize the multiplication process and check your answers.

Practicing with Different Types of Binomials

To become proficient at multiplying binomials, it's essential to practice with different types of binomials. Some examples include:

• Binomials with two variables (e.g., (x + y)(x + 5))
• Binomials with one variable and a constant (e.g., (x + 3)(x + 2))
• Binomials with two constants (e.g., (3 + 2)(4 + 5))

Conclusion: Mastering Multiplying Binomials

Multiplying binomials is a fundamental concept in algebra that can be mastered with practice and the right strategies. By using the FOIL method, box method, distributive property, grid method, algebra tiles, online tools, and practicing with different types of binomials, you can become proficient at multiplying binomials.

We hope this article has helped you understand the different ways to master multiplying binomials. Do you have any favorite techniques for multiplying binomials? Share them with us in the comments below!