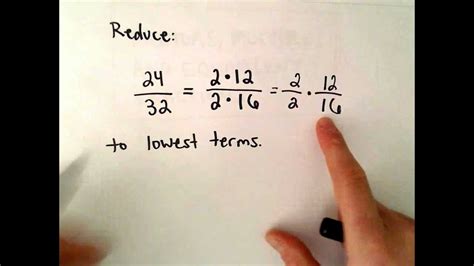Simplifying 55: Reduce To Lowest Terms

Quick Links :

Simplifying Fractions: Reduce To Lowest Terms

When it comes to working with fractions, one of the most important concepts to understand is how to simplify them. Simplifying fractions means reducing them to their lowest terms, which can make it easier to add, subtract, multiply, and divide them. In this article, we'll explore the concept of simplifying fractions and provide tips and examples to help you master this essential math skill.

Fractions are a way of representing part of a whole, and they consist of two parts: the numerator (the top number) and the denominator (the bottom number). When you simplify a fraction, you're finding an equivalent fraction with a smaller numerator and denominator. This can be useful in a variety of situations, such as when you're adding or subtracting fractions with different denominators.

Why Simplify Fractions?

Simplifying fractions is important for several reasons. Firstly, it makes it easier to compare fractions. When fractions are in their lowest terms, it's simpler to determine which one is larger or smaller. Secondly, simplifying fractions can make calculations easier. When you're working with fractions that are in their lowest terms, you can avoid errors and make calculations more efficient.

How to Simplify Fractions

Simplifying fractions is a straightforward process that involves finding the greatest common divisor (GCD) of the numerator and denominator. Here are the steps to follow:

1. Find the greatest common divisor (GCD): The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. You can find the GCD by listing the factors of the numerator and denominator and identifying the largest common factor.
2. Divide the numerator and denominator by the GCD: Once you've found the GCD, divide both the numerator and denominator by this number. This will give you a new fraction with a smaller numerator and denominator.
3. Check if the fraction is in its lowest terms: After simplifying the fraction, check if it's in its lowest terms by ensuring that the numerator and denominator have no common factors other than 1.

Examples of Simplifying Fractions

Let's take a look at some examples of simplifying fractions:

• Example 1: Simplify the fraction 6/8.
  • Find the GCD of 6 and 8, which is 2.
  • Divide the numerator and denominator by 2, giving you 3/4.
• Example 2: Simplify the fraction 12/16.
  • Find the GCD of 12 and 16, which is 4.
  • Divide the numerator and denominator by 4, giving you 3/4.
• Example 3: Simplify the fraction 24/30.
  • Find the GCD of 24 and 30, which is 6.
  • Divide the numerator and denominator by 6, giving you 4/5.

Real-World Applications of Simplifying Fractions

Simplifying fractions has a range of real-world applications, including:

• Cooking: When following a recipe, you may need to simplify fractions to ensure that you're using the correct quantities of ingredients.
• Building and construction: Architects and builders use fractions to calculate measurements and quantities of materials. Simplifying fractions can help them avoid errors and ensure that their calculations are accurate.
• Finance: Fractions are used in finance to calculate interest rates, investment returns, and other financial metrics. Simplifying fractions can help financial professionals make more accurate calculations and avoid errors.

Common Mistakes to Avoid When Simplifying Fractions

When simplifying fractions, there are several common mistakes to avoid:

• Not finding the greatest common divisor: Failing to find the GCD can result in a fraction that's not in its lowest terms.
• Dividing the numerator and denominator by the wrong number: Make sure you're dividing both numbers by the same number to avoid errors.
• Not checking if the fraction is in its lowest terms: Always check that the numerator and denominator have no common factors other than 1 to ensure that the fraction is in its lowest terms.

Conclusion

Simplifying fractions is an essential math skill that can make calculations easier and more efficient. By following the steps outlined in this article, you can master the art of simplifying fractions and apply it to a range of real-world situations. Remember to always find the greatest common divisor, divide the numerator and denominator by the correct number, and check if the fraction is in its lowest terms to avoid common mistakes.