486 In Expanded Form: 4 Easy Steps To Master It

Quick Links :

Mastering numbers in expanded form is a fundamental skill that helps build a strong foundation in mathematics, particularly in arithmetic operations and place value understanding. One of the numbers that students often encounter is 486. Breaking down this number into its expanded form not only enhances understanding but also aids in performing calculations more accurately. In this article, we'll delve into the steps to express 486 in expanded form and explore the concept in depth.

Understanding Expanded Form

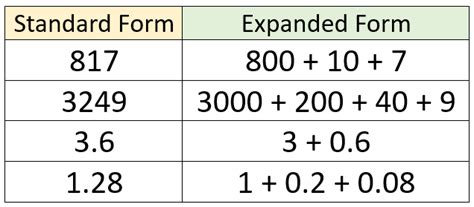
Expanded form is a way of writing numbers to show the value of each digit. It involves expressing a number as the sum of its place values, with each place value multiplied by its corresponding digit. This method is invaluable for teaching the concept of place value and making arithmetic operations more intuitive.

Benefits of Learning Expanded Form

• Enhances Place Value Understanding: Learning to write numbers in expanded form solidifies the concept of place value, where each digit in a number holds a specific value based on its position.
• Improves Arithmetic Skills: Expanded form aids in understanding how numbers are built from their constituent parts, making addition, subtraction, multiplication, and division more comprehensible.
• Develops Problem-Solving Skills: By breaking down numbers into their expanded form, students develop a more nuanced approach to solving arithmetic problems.

Steps to Master 486 in Expanded Form

Expressing 486 in expanded form involves understanding the place value of each digit within the number. Here are the steps:

Step 1: Identify the Place Value of Each Digit

The number 486 can be broken down as follows:

• 4 is in the hundreds place.
• 8 is in the tens place.
• 6 is in the ones place.

Step 2: Multiply Each Digit by Its Place Value

Now, we multiply each digit by the value of its place:

• 4 (hundreds place) = 4 * 100 = 400
• 8 (tens place) = 8 * 10 = 80
• 6 (ones place) = 6 * 1 = 6

Step 3: Combine the Values

To get the expanded form, we combine these values: 400 + 80 + 6 = 486

Step 4: Write in Expanded Form

Thus, the expanded form of 486 is 400 + 80 + 6.

Practical Applications of Expanded Form

Understanding and applying expanded form in arithmetic operations can simplify complex calculations. For example, adding or subtracting numbers becomes more manageable when the numbers are broken down into their expanded forms, as it allows for a clearer understanding of the values being manipulated.

Example: Adding 486 and 279 Using Expanded Form

• 486 in expanded form is 400 + 80 + 6.
• 279 in expanded form is 200 + 70 + 9.
• Adding these together: (400 + 200) + (80 + 70) + (6 + 9) = 600 + 150 + 15 = 765.

Conclusion and Next Steps

Mastering the concept of expanded form, as demonstrated with the number 486, is a crucial step in building a strong foundation in mathematics. By understanding and applying this concept, students can enhance their arithmetic skills and develop a more profound appreciation for the structure of numbers.

If you're looking to further explore or practice the concept of expanded form, consider the following:

• Engage in exercises where you convert various numbers into their expanded forms.
• Practice arithmetic operations using numbers in expanded form.
• Explore how expanded form relates to other mathematical concepts, such as decimals and fractions.

By taking these steps and continuing to practice, you'll not only master the expanded form of 486 but also solidify your understanding of numbers and their manipulation.

We hope this article has been informative and helpful. Feel free to share your thoughts or ask questions in the comments section below!