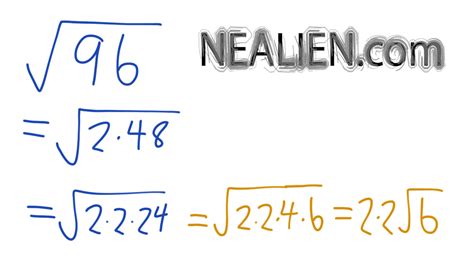Simplifying 4 Square Root Of 96 In Radical Form

Quick Links :

Simplifying square roots is an essential skill in mathematics, and it's used extensively in various mathematical operations, including algebra, geometry, and calculus. The square root of a number is a value that, when multiplied by itself, gives the original number. In this article, we'll explore how to simplify the 4 square root of 96 in radical form.

Understanding Square Roots and Radicals

Before diving into the simplification process, let's quickly review what square roots and radicals are. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16. A radical is a symbol used to represent a square root, and it's denoted by the symbol √.

The Importance of Simplifying Square Roots

Simplifying square roots is crucial in mathematics because it helps to express numbers in their most basic form. This, in turn, makes it easier to perform mathematical operations, such as addition, subtraction, multiplication, and division. Simplifying square roots also helps to identify patterns and relationships between numbers, which is essential in algebra and geometry.

Step-by-Step Guide to Simplifying the 4 Square Root of 96

Now, let's move on to simplifying the 4 square root of 96 in radical form. To do this, we'll follow these steps:

Step 1: Factorize the Number 96

The first step is to factorize the number 96 into its prime factors. The prime factorization of 96 is:

96 = 2 × 2 × 2 × 2 × 2 × 3

Step 2: Identify the Perfect Squares

Next, we need to identify the perfect squares in the prime factorization of 96. A perfect square is a number that can be expressed as the square of an integer. In this case, we can see that:

96 = 2^5 × 3 = (2^4) × 2 × 3 = (2^2)^2 × 2 × 3

Step 3: Simplify the Radical

Now, we can simplify the radical by taking out the perfect squares:

√96 = √((2^2)^2 × 2 × 3) = √(4^2 × 2 × 3) = 4√(2 × 3) = 4√6

Therefore, the simplified form of the 4 square root of 96 in radical form is 4√6.

Practical Applications of Simplifying Square Roots

Simplifying square roots has numerous practical applications in various fields, including:

• Geometry: Simplifying square roots is essential in geometry, where it's used to calculate the length of sides and diagonals of triangles and quadrilaterals.
• Algebra: Simplifying square roots is used extensively in algebra, where it's used to solve quadratic equations and inequalities.
• Physics: Simplifying square roots is used in physics to calculate distances, velocities, and accelerations.
• Engineering: Simplifying square roots is used in engineering to design and optimize systems, such as bridges and buildings.

Conclusion

Simplifying square roots is an essential skill in mathematics, and it's used extensively in various mathematical operations. By following the steps outlined in this article, you can simplify the 4 square root of 96 in radical form to 4√6. Remember, simplifying square roots helps to express numbers in their most basic form, making it easier to perform mathematical operations and identify patterns and relationships between numbers.