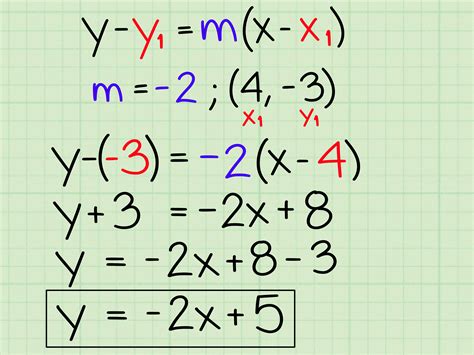Writing Equations In Standard And Slope-Intercept Form Made Easy

Quick Links :

Equations are the backbone of mathematics, and understanding how to write them is crucial for problem-solving in various fields, including physics, engineering, and economics. When it comes to linear equations, there are two main forms: standard form and slope-intercept form. In this article, we will explore both forms, explain their significance, and provide practical examples to help you master writing equations in standard and slope-intercept form.

The Importance of Linear Equations

Linear equations are used to model real-world situations, such as the cost of goods, the distance traveled by an object, and the rate of change of a quantity. They are essential in mathematics, science, and engineering, and are used to solve problems involving rates of change, optimization, and graphing. By understanding how to write linear equations in standard and slope-intercept form, you will be able to tackle complex problems with ease and accuracy.

Standard Form: The Foundation of Linear Equations

Standard form, also known as the general form, is the most basic way to write a linear equation. The standard form of a linear equation is:

Ax + By = C

where:

• A and B are coefficients (numbers that are multiplied by the variables)
• x and y are variables (letters that represent unknown values)
• C is the constant term (a number that is not multiplied by a variable)

For example, the equation 2x + 3y = 5 is in standard form.

Slope-Intercept Form: The Graphical Representation

Slope-intercept form, also known as the slope-point form, is another way to write a linear equation. The slope-intercept form of a linear equation is:

y = mx + b

where:

• m is the slope (a measure of how steep the line is)
• b is the y-intercept (the point where the line crosses the y-axis)
• x is the variable (a letter that represents an unknown value)

For example, the equation y = 2x + 3 is in slope-intercept form.

Converting Standard Form to Slope-Intercept Form

To convert a linear equation from standard form to slope-intercept form, we need to isolate the variable y. This can be done by subtracting the term with x from both sides of the equation.

For example, let's convert the equation 2x + 3y = 5 from standard form to slope-intercept form:

2x + 3y = 5

Subtract 2x from both sides:

3y = -2x + 5

Divide both sides by 3:

y = (-2/3)x + 5/3

Now, the equation is in slope-intercept form.

Converting Slope-Intercept Form to Standard Form

To convert a linear equation from slope-intercept form to standard form, we need to multiply both sides of the equation by the coefficient of x and then rearrange the terms.

For example, let's convert the equation y = 2x + 3 from slope-intercept form to standard form:

y = 2x + 3

Multiply both sides by 1 (the coefficient of x):

y = 2x + 3

Subtract 2x from both sides:

-2x + y = 3

Now, the equation is in standard form.

Practical Examples and Applications

Linear equations in standard and slope-intercept form have numerous applications in real-world problems. Here are a few examples:

• Cost of Goods: A company produces two products, A and B, with a cost of $2 and $3 per unit, respectively. The total cost of producing x units of A and y units of B is $1000. Write a linear equation in standard form to represent the cost.
• Distance Traveled: A car travels from city A to city B at an average speed of 60 miles per hour. The distance between the two cities is 200 miles. Write a linear equation in slope-intercept form to represent the distance traveled.

Solving Linear Equations

Linear equations can be solved using various methods, including graphing, substitution, and elimination. Here are a few examples:

• Graphing: Graph the linear equation y = 2x + 3 on a coordinate plane. Find the x-intercept and y-intercept.
• Substitution: Solve the system of linear equations x + 2y = 4 and 3x - 2y = -2 using substitution.

Conclusion: Mastering Standard and Slope-Intercept Form

Writing linear equations in standard and slope-intercept form is an essential skill in mathematics, science, and engineering. By understanding the difference between these two forms, you can tackle complex problems with ease and accuracy. With practice and patience, you can master writing linear equations in standard and slope-intercept form and become proficient in solving problems that involve rates of change, optimization, and graphing.