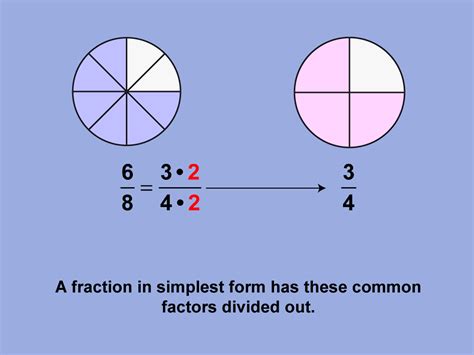
The importance of fractions in mathematics cannot be overstated. Fractions are a fundamental concept in arithmetic, and understanding how to work with them is crucial for success in various mathematical disciplines. In this article, we will explore the concept of 23 as a fraction in simplest form.
What is a Fraction?

A fraction is a mathematical expression that represents a part of a whole. It consists of two parts: the numerator and the denominator. The numerator represents the number of equal parts, while the denominator represents the total number of parts. For example, in the fraction 3/4, the numerator is 3, and the denominator is 4.
What is the Importance of Simplifying Fractions?
Simplifying fractions is essential in mathematics because it helps to:
- Reduce complexity: Simplifying fractions makes it easier to work with them, especially when performing arithmetic operations.
- Avoid confusion: Simplified fractions reduce the risk of errors and confusion when working with fractions.
- Improve accuracy: Simplifying fractions ensures that calculations are accurate and reliable.
How to Simplify a Fraction

To simplify a fraction, you need to find the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both numbers without leaving a remainder. Once you have found the GCD, you can divide both the numerator and the denominator by the GCD to simplify the fraction.
Example: Simplifying 23 as a Fraction
To simplify 23 as a fraction, we need to find the GCD of 23 and 1. Since 23 is a prime number, its GCD with 1 is 1. Therefore, the simplest form of 23 as a fraction is 23/1.
Benefits of Simplifying Fractions

Simplifying fractions has several benefits, including:
- Improved accuracy: Simplified fractions reduce the risk of errors and ensure accurate calculations.
- Increased efficiency: Simplifying fractions saves time and effort when performing arithmetic operations.
- Better understanding: Simplified fractions help to develop a deeper understanding of mathematical concepts and relationships.
Real-World Applications of Simplifying Fractions
Simplifying fractions has numerous real-world applications, including:
- Cooking and recipe scaling
- Financial calculations and budgeting
- Scientific measurements and data analysis
- Engineering and architecture
Conclusion: Embracing the Power of Simplified Fractions

In conclusion, simplifying fractions is an essential skill in mathematics that offers numerous benefits and real-world applications. By understanding how to simplify fractions, you can improve your accuracy, efficiency, and understanding of mathematical concepts. Remember, 23 as a fraction in simplest form is 23/1.
We hope this article has provided you with a deeper understanding of fractions and the importance of simplifying them. If you have any questions or comments, please feel free to share them below.
What is the definition of a fraction?
+A fraction is a mathematical expression that represents a part of a whole, consisting of a numerator and a denominator.
Why is simplifying fractions important?
+Simplifying fractions is essential to reduce complexity, avoid confusion, and improve accuracy in mathematical calculations.
How do you simplify a fraction?
+To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator, and divide both numbers by the GCD.