0.22 As A Fraction In Simplest Form

Quick Links :

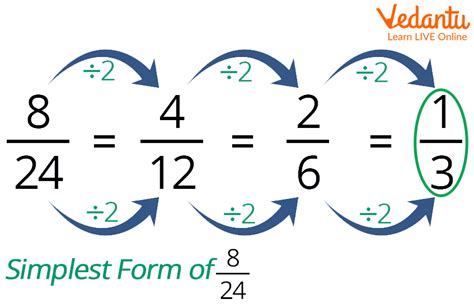
The decimal number 0.22 can be expressed as a fraction in simplest form. To do this, we can write 0.22 as 22/100 and then simplify the fraction.

22 and 100 have a common factor of 2, so we can divide both the numerator and the denominator by 2 to get:

22 ÷ 2 = 11 100 ÷ 2 = 50

So, 0.22 as a fraction in simplest form is 11/50.

Understanding Decimals and Fractions

Decimals and fractions are two different ways of representing numbers. Decimals are a way of expressing numbers using a point to separate the whole part from the fractional part. Fractions, on the other hand, are a way of expressing numbers as a ratio of two integers.

For example, the decimal number 0.5 can be expressed as the fraction 1/2. Similarly, the decimal number 0.25 can be expressed as the fraction 1/4.

Decimals and fractions are used in various mathematical operations, such as addition, subtraction, multiplication, and division. Understanding how to convert between decimals and fractions is an important skill in mathematics.

Converting Decimals to Fractions

Converting decimals to fractions is a straightforward process. Here are the steps:

1. Write the decimal number as a fraction with the decimal part as the numerator and the place value of the last digit as the denominator.
2. Simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD).

For example, let's convert the decimal number 0.36 to a fraction.

Step 1: Write the decimal number as a fraction. 0.36 = 36/100

Step 2: Simplify the fraction. 36 and 100 have a common factor of 4, so we can divide both the numerator and the denominator by 4. 36 ÷ 4 = 9 100 ÷ 4 = 25

So, 0.36 as a fraction in simplest form is 9/25.

Examples of Converting Decimals to Fractions

Here are some examples of converting decimals to fractions:

• 0.5 = 1/2
• 0.25 = 1/4
• 0.75 = 3/4
• 0.125 = 1/8

Note that some decimals may not have a simple fraction equivalent. For example, the decimal number 0.123456789 cannot be expressed as a simple fraction.

Real-World Applications of Decimals and Fractions

Decimals and fractions have many real-world applications. Here are a few examples:

• Measurement: Decimals and fractions are used to measure lengths, weights, and volumes. For example, a recipe may call for 3/4 cup of flour, which can be measured using a decimal scale (0.75 cups).
• Finance: Decimals and fractions are used in finance to calculate interest rates, investment returns, and currency exchange rates.
• Science: Decimals and fractions are used in science to express measurements and quantities, such as the concentration of a solution (e.g., 0.5 M) or the ratio of reactants in a chemical reaction.

Understanding decimals and fractions is essential for solving problems in these fields.

Conclusion

In conclusion, the decimal number 0.22 can be expressed as a fraction in simplest form as 11/50. Understanding decimals and fractions is an important skill in mathematics, and converting between the two is a straightforward process. Decimals and fractions have many real-world applications, and being able to work with them is essential for solving problems in fields such as measurement, finance, and science.

We hope this article has been informative and helpful. If you have any questions or comments, please feel free to ask.